[江苏]2013届江苏省无锡市北塘区九年级中考二模数学试卷
保护水资源,人人有责.我国是缺水国家,目前可利用淡水资源总量仅约为899000亿m3,数据899000用科学记数法表示为( )
| A.8.99×105 | B.0.899×106 | C.8.99×104 | D.89.9×104 |
如果一个多边形的内角和等于外角和的3倍,那么这个多边形的边数为( )
| A.7 | B.8 | C.9 | D.10 |
如图,点O在⊙A外,点P在线段OA上运动.以OP为半径的⊙O与⊙A的位置关系不可能是下列中的( )
| A.外离 | B.外切 | C.相交 | D.内含 |
一张等腰三角形纸片,底边长l5cm,底边上的高长22.5cm.现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,如图所示.已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
| A.第4张 | B.第5张 | C.第6张 | D.第7张 |
古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”,而把1、4、9、16 … 这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
| A.13 = 3+10 | B.25 = 9+16 | C.49=21+28 | D.49 = 18+31 |
如图,Rt△ABC的直角边BC在x轴的正半轴上,斜边AC上的中线BD的反向延长线交y轴的负半轴于点E,双曲线 经过点A,若△BEC的面积为5,则k的值为( )
经过点A,若△BEC的面积为5,则k的值为( )
A. |
B.5 | C.10 | D. |
如图1,表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A,且当钟面显示3点30分时,分针垂直于桌面,点A距桌面的高度为10cm.如图2,若此钟面显示3点45分时,点A距桌面的高度为16cm,则钟面显示3点50分时,点A距桌面的高度为 cm.
如图,规定程序运行到“结果是否大于33”为一次运算,且运算进行3次才停止,则可输入的实数x的取值范围为 .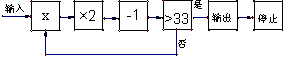
如图,有一无盖的长方体盒子,高为9cm,底面是边长为12cm的正方形,现在有一只蚂蚁(A点)在盒子外部距离下底面2cm的一条高上,而在盒子内部距离上底面3cm处有一饼干屑(B点),A点和B点在不相邻的两条高上,若蚂蚁能吃到饼干屑,则爬行的最短路程为 cm.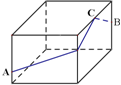
如图,在□ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)试说明:AB=CF;
(2)连接DE,若AD=2AB,试说明:DE⊥AF.
在无锡市首届“文明风尚好少年”全媒体选拔大赛初赛中,甲、乙、丙三位评委对小选手的综合表现,分别给出“待定”(用字母W表示)或“通过”(用字母P表示)的结论.
(1)请用树状图表示出三位评委给小选手乐乐的所有可能的结论;
(2)对于小选手乐乐,只有甲、乙两位评委给出相同结论的概率是多少?
(3)比赛规定,三位评委中至少有两位给出“通过”的结论,则小选手可入围进入复赛,问乐乐进入复赛的概率是多少?
对某校八年级随机抽取若干名学生进行体能测试,成绩按A、B、C、D四个等级进行了评定.现将抽取学生的成绩评定结果进行分析,并绘制扇形统计图和条形统计图如下: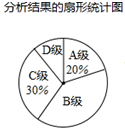
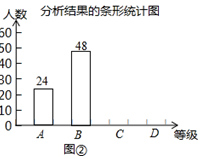
根据上述信息完成下列问题:
(1)这次抽取的样本的容量为 ;
(2)请在图②中把条形统计图补充完整;
(3)图①中“D级”对应的扇形圆心角度数为 °;
(4)已知该校八年级共有学生750名,请你估计体能达到A级和B级的共约有 人.
如图,图甲是一个水桶模型示意图,水桶提手结构的平面图是轴对称图形.当点O到BC(或DE)的距离大于或等于⊙O的半径时(⊙O是桶口所在圆,半径为OA),提手才能从图甲的位置转到图乙的位置,这样的提手才合格.现用金属材料做了一个水桶提手ABCDEF(如图丙,其中CD是弧,其余是线段),O是AF的中点,桶口直径AF = cm,AB=FE=5cm,∠ABC ="∠FED" =130°.请通过计算判断这个水桶提手是否合格.(参考数据:
cm,AB=FE=5cm,∠ABC ="∠FED" =130°.请通过计算判断这个水桶提手是否合格.(参考数据: ≈1.73,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75.)
≈1.73,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75.)
|

由于受到手机更新换代的影响,某手机店经销的甲品牌手机二月售价比一月每部降价500元.如果卖出相同数量的甲品牌手机,那么一月销售额为4.5万元,二月销售额只有4万元.
(1)一月甲品牌手机每部售价为多少元?
(2)为了提高利润,该店计划三月购进乙品牌手机销售,已知甲品牌每部进价为3500元,乙品牌每部进价为4000元,预计用不多于7.5万元且不少于7.4万元的资金购进这两种手机共20部,请问有哪几种进货方案?
(3)该店三月营销计划为:在二月售价基础上每售出一部甲品牌手机再返还顾客话费a元,而乙品牌按每部4400元销售,如果要使(2)中所有进货方案获利都相同,a应取何值?
如图,抛物线 与直线AB交于点A(-1,0),B(4,
与直线AB交于点A(-1,0),B(4, ).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
(1)求抛物线的解析式;
(2)设点D的横坐标为m,则用m的代数式表示线段DC的长;
(3)在(2)的条件下,若△ADB的面积为S,求S关于m的函数关系式,并求出当S取最大值时的点C的坐标;
(4)当点D为抛物线的顶点时,若点P是抛物线上的动点,点Q是直线AB上的动点,判断有几个位置能使以点P,Q,C,D为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连结DG.设点D运动的时间为t秒.

(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值;
(3)以DH所在直线为对称轴,线段AC经轴对称变换后的图形为A′C′.当t> 时,连结C ′C,则以CC´为直径的圆何时与直线AB相切?
时,连结C ′C,则以CC´为直径的圆何时与直线AB相切?
如图1,已知有一张三角形纸片ABC的一边AB=10,若D为AB边上的点,过点D作DE//BC交AC于点E,分别过点D、E作DF⊥BC,EG⊥BC,垂足分别为点F、点G,把三角形纸片ABC分别沿DE、DF、EG按图1方式折叠,点A、B、C分别落在A´、B´、C´处.若A´、B´、C´在矩形DFGE内或者其边上,且互不重合,此时我们称△A´B´C´(即图中阴影部分)为“重叠三角形”.





(1)实验操作:当AD=4时,①若∠A=90°,AB=AC,请在图2中画出“重叠三角形”, = ;
= ;
②若AB=AC,BC=12,如图3, = ;③若∠B=30°,∠C=45°,如图4,
= ;③若∠B=30°,∠C=45°,如图4, = ;
= ;
(2)实验探究:若△ABC为等边三角形(如图5),设AD的长为m,若重叠三角形A´B´C´存在,试用含m的代数式表示重叠三角形A´B´C´的面积,并写出m的取值范围.






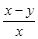 ,
,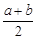 ,
,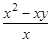 ,
,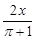 ,
,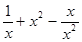 中,分式的个数是( )
中,分式的个数是( )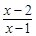 在实数范围内有意义,则x的取值范围是 .
在实数范围内有意义,则x的取值范围是 .

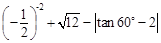 ;
;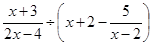 其中
其中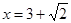 .
. ;(2)求不等式组
;(2)求不等式组 的整数解.
的整数解. 粤公网安备 44130202000953号
粤公网安备 44130202000953号