[上海]2013届上海市虹口区中考二模数学试卷
在平面直角坐标系 中,直线
中,直线 经过
经过
| A.第一、二、三象限; | B.第一、二、四象限; |
| C.第一、三、四象限; | D.第二、三、四象限. |
某小区20户家庭某月的用电量如下表所示:
| 用电量(度) |
120 |
140 |
160 |
180 |
200 |
| 户数 |
2 |
3 |
6 |
7 |
2 |
则这20户家庭该月用电量的众数和中位数分别是
A.180,160; B.160,180; C.160,160; D.180,180.
已知两圆内切,圆心距为5,其中一个圆的半径长为8 ,那么另一个圆的半径长是
| A.3; | B.13; | C.3或13; | D.以上都不对. |
在下列命题中,属于假命题的是
| A.对角线相等的梯形是等腰梯形; |
| B.两腰相等的梯形是等腰梯形; |
| C.底角相等的梯形是等腰梯形; |
| D.等腰三角形被平行于底边的直线截成两部分,所截得的四边形是等腰梯形. |
在一个不透明的盒子中装有8个白球和若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出1个球,它恰好是白球的概率是 ,则该盒中黄球的个数为 .
,则该盒中黄球的个数为 .
为了解某校九年级学生体能情况,随机抽查了其中的25名学生,测试了1分钟仰卧起坐的次数,并绘制成频数分布直方图(如图所示),那么仰卧起坐的次数在20~25的频率是 .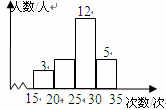
将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍得△AB′ C′ ,即如图①,∠BAB′=θ, ,我们将这种变换记为[θ,n] .如图②,在△DEF中,∠DFE=90°,将△DEF绕点D旋转,作变换[60°,n]得△DE′F′,如果点E、F、F′恰好在同一直线上,那么n= .
,我们将这种变换记为[θ,n] .如图②,在△DEF中,∠DFE=90°,将△DEF绕点D旋转,作变换[60°,n]得△DE′F′,如果点E、F、F′恰好在同一直线上,那么n= .


如图,在直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°,点F是CD边上一点,将纸片沿BF折叠,点C落在E点,使直线BE经过点D,若BF=CF=8,则AD的长为 .
如图,在△ABC中,AB=AC=10, ,圆O经过点B、C,圆心O在△ABC的内部,且到点A的距离为2,求圆O的半径.
,圆O经过点B、C,圆心O在△ABC的内部,且到点A的距离为2,求圆O的半径.
某超市进了一批成本为6元/个的文具.调查后发现:这种文具每周的销售量y(个)与销售价x(元/个)之间的关系满足一次函数关系,如下表所示:
| 销售价x(元/个) |
8 |
9.5 |
11 |
14 |
| 销售量y(个) |
220 |
205 |
190 |
160 |
(1)求y与x之间的函数解析式(不必写出定义域);
(2)已知该超市这种文具每周的销售量不少于60个,若该超市某周销售这种文具(不考虑其它因素)的利润为800元,求该周每个文具的销售价.
已知:如图,在正方形ABCD中,点E、F分别在边BC和CD上,∠BAE=∠DAF.
(1)求证:BE=DF;
(2)联结AC交EF于点O,延长OC至点M,使OM= OA,联结EM、FM.求证:四边形AEMF是菱形.
已知:直线 交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线
交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线 经过点A、B、C.
经过点A、B、C.
(1)求该抛物线的表达式;
(2)点D的坐标为(-3,0),点P为线段AB上一点,当锐角∠PDO的正切值为 时,求点P的坐标;
时,求点P的坐标;
(3)在(2)的条件下,该抛物线上的一点E在x轴下方,当△ADE的面积等于四边形APCE的面积时,求点E的坐标.
 ;
; ;
; ;
; .
. ;
; ;
; ;
; .
. .
. 的解集是 .
的解集是 . 时,如果设
时,如果设 ,那么原方程化为关于
,那么原方程化为关于 的整式方程可以是 .
的整式方程可以是 . 的解是 .
的解是 . ,若在每个象限内,y随x的增大而增大,则k的取值范围是 .
,若在每个象限内,y随x的增大而增大,则k的取值范围是 . 向左平移2个单位,所得抛物线的表达式为 .
向左平移2个单位,所得抛物线的表达式为 . ,
, ,则用向量
,则用向量 、
、 表示向量
表示向量 为 .
为 . ,其中
,其中 .
.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号