天津市六校高三第三次联考试题数学文
已知函数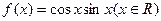 ,给出下列四个命题:
,给出下列四个命题:
①若
②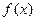 的最小正周期是
的最小正周期是 ;
;
③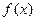 在区间
在区间 上是增函数;
上是增函数;
④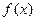 的图象关于直线
的图象关于直线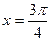 对称;
对称;
⑤当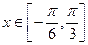 时,
时,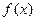 的值域为
的值域为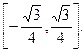
其中正确的命题为 (  )
)
| A.①②④ | B.③④⑤ | C.②③ | D.③④ |
为了保护环境,发展低碳经济,2010年全国“两会”
使用的记录纸、笔记本、环保袋、手提袋等均是以石
灰石为原料生产的石头纸用品,已知某单位每月石头
纸用品的产量最少为300吨,最多为500吨,每月成
本y(元)与每月产量x(吨)之间的函数关系可近似
的表示为: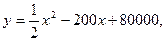 若要使每吨的平
若要使每吨的平
均成本最低,则该单位每月产量应为 吨.
(本小题满分12分)
设O为坐标原点,点P的坐标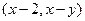
(I)在一个盒子中,放有标号为1,2,3的三张卡片,现从此盒中有放回地先后抽到两张卡片的标号分别记为x,y,求|OP|的最
 大值,并求事件“|OP|取到最大值”的概率;
大值,并求事件“|OP|取到最大值”的概率;
(II)若利用计算机随机在[0,3]上先后取两个数分别记为x,y,求P点在第一象限的概率.
(本小题满分12分)
如图,在四棱锥S—ABCD中,底面ABCD为矩形,SA⊥平面ABCD,二面角S—
CD—A的平面角为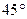 ,M为AB中点,N为SC中点.
,M为AB中点,N为SC中点.
(1)证明:MN//平面SAD;
(2)证明:平面SMC⊥平面SCD;
|
(3)若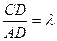 ,求实数
,求实数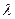 的值,使得直线SM与平面SCD所成角为
的值,使得直线SM与平面SCD所成角为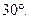
(本小题满分14分)
设函数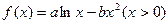
(1)若函数 在x=1处与直线
在x=1处与直线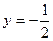 相切
相切
①求实数a,b的值;
②求函数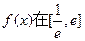 上的最大值.
上的最大值.
(2)当b=0时,若不等式 对所有的
对所有的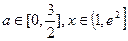 都成立,求
都成立,求 实数m的取值范围.
实数m的取值范围.
 ,且
,且 为纯虚数,则a等于 ( )
为纯虚数,则a等于 ( )

 ,则
,则 的最小值是 ( )
的最小值是 ( ) 的右焦点与抛物线
的右焦点与抛物线 的焦点重合,则该双曲线的离心率为 ( )
的焦点重合,则该双曲线的离心率为 ( )



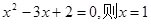 ”的逆否命题为:“若
”的逆否命题为:“若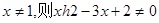 ”
”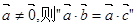 是“
是“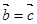 ”的充要条件
”的充要条件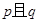 ”为假命题,则p、q至少有一个为假命题
”为假命题,则p、q至少有一个为假命题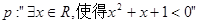 ,则
,则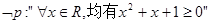
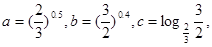 则 ( )
则 ( ) ,则
,则 的值为 ( )
的值为 ( )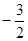

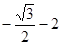
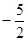
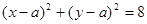 上总存在两个点到原点的距离为
上总存在两个点到原点的距离为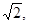 则实数a的取值范围是 ( )
则实数a的取值范围是 ( )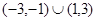
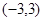

 则函数
则函数 的解析式为 ( )
的解析式为 ( )



 满足
满足 若
若 则数列
则数列 为 ( )
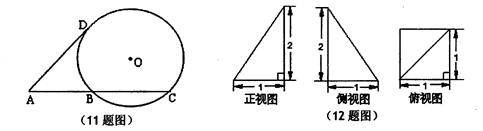
为 ( )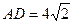 ,圆O的半径r=AB=4,则圆心O到AC的距离为
,圆O的半径r=AB=4,则圆心O到AC的距离为  .
.

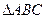 的重心,若AB=2,AC=4,则
的重心,若AB=2,AC=4,则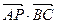 = .
= . 的解集为
的解集为 ,且
,且 ,则a的取值集合
,则a的取值集合 为 .
为 .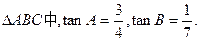
 ,求BC边的长.
,求BC边的长.
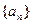 的前n项和为
的前n项和为 ,且满足
,且满足
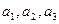 的值;
的值; 的前n项和为
的前n项和为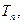 求满足不等式
求满足不等式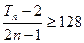 的最小n值.
的最小n值. 过点
过点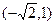 ,长轴长为
,长轴长为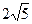 ,过点C(-1,0)且斜率为k的直线l与椭圆相交于不同的两点A、B.
,过点C(-1,0)且斜率为k的直线l与椭圆相交于不同的两点A、B.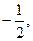 求直线l的斜率;
求直线l的斜率; 是与k无关的常数?若存在,求出点M的坐标;若不存在,请说明理由.
是与k无关的常数?若存在,求出点M的坐标;若不存在,请说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号