东北三校高三下学期第一次联考数学试题
下列命题错误的是( )
A.对于命题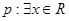 ,使得 ,使得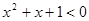 ,则 ,则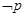 为: 为: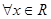 ,均有 ,均有 |
B.命题“若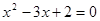 ,则 ,则 ”的逆否命题为“若 ”的逆否命题为“若 ,则 ,则 ” ” |
C.若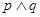 为假命题,则 为假命题,则 均为假命题 均为假命题 |
D.“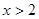 ”是“ ”是“ ”的充分不必要条件 ”的充分不必要条件 |
某铁路客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过 按
按 元/
元/ 收费,超过
收费,超过 的部分按
的部分按 元/
元/ 收费.相应收费系统的流程图如右图所示,则①处应填( )
收费.相应收费系统的流程图如右图所示,则①处应填( )
A. |
B. |
C. |
D. |
甲乙两位同学在高三的5次月考中数学成绩统计如茎叶图所示,若甲乙两人的平均成绩分别是 ,则下列正确的
,则下列正确的 是( )
是( )
A. ;乙比甲成绩稳定 ;乙比甲成绩稳定 |
B. ;甲比乙成绩稳定 ;甲比乙成绩稳定 |
C. ;乙比甲成绩稳定 ;乙比甲成绩稳定 |
D. ;甲比乙成绩稳定 ;甲比乙成绩稳定 |
设 、
、 是两个不同的平面,
是两个不同的平面, 、
、 是两条不同的直线,给出下列4个命题,其中正确命题是( )
是两条不同的直线,给出下列4个命题,其中正确命题是( )
A.若 ∥ ∥ , , ∥ ∥ ,则 ,则 ∥ ∥  |
B.若 ∥ ∥ , , ∥ ∥ , , ∥ ∥ ,则 ,则 ∥ ∥ ; ; |
C.若 ⊥ ⊥ , , ⊥ ⊥ , , ⊥ ⊥ ,则 ,则 ⊥ ⊥ ; ; |
D.若 、 、 在平面 在平面 内的射影互相垂直,则 内的射影互相垂直,则 ⊥ ⊥ . . |
已知函数 ,对于满足
,对于满足 的任意
的任意 ,给出下列结论:(1)
,给出下列结论:(1) ;(2)
;(2) ;(3)
;(3) ;(4)
;(4) ,其中正确结论的序号是( )
,其中正确结论的序号是( )
| A.(1)(2) | B.(1)(3) | C.(2)(4) | D.(3)(4) |
圆 的方程为
的方程为 ,圆
,圆 的方程为
的方程为
 ,过圆
,过圆 上任意一点
上任意一点 作圆
作圆 的两条切线
的两条切线 、
、 ,切点分别为
,切点分别为 、
、 ,则
,则 的最小值是 ( )
的最小值是 ( )
| A.12 | B.10 | C.6 | D.5 |
若不等式组 表示的平面区域为
表示的平面区域为 ,
, 所表示的平面区域为
所表示的平面区域为 ,现随机向区域
,现随机向区域 内抛一粒豆子,则豆子落在区域
内抛一粒豆子,则豆子落在区域 内的概率为____________________.
内的概率为____________________.
(1)由“若 则
则 ”类比“若
”类比“若 为三个向量则
为三个向量则 ”
”
(2)在数列 中,
中, 猜想
猜想
(3)在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”
(4)已知 ,则
,则 .
.
上述四个推理中,得出的结论正确的是____ .(写出所有正确结论的序号)
甲乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7,8,9,10环,且每次射击成绩互不影响,射击环数的频率分布表如 下,
下,
甲运动员
| 射击环数 |
频数 |
频率 |
| 7 |
10 |
0.1 |
| 8 |
10 |
0.1 |
| 9 |
 |
0.45 |
| 10 |
35 |
 |
| 合计 |
 100 100 |
1 |
乙运动员
| 射击环数 |
频数 |
频率 |
| 7 |
8 |
0.1 |
| 8 |
12 |
0.15 |
| 9 |
 |
|
| 10 |
|
0.35 |
| 合计 |
80 |
1 |
若将频率视为概率,回答下列问题,
(1)求甲运动员击中10环的概率
(2)求甲运动员在3次射击中至少有一次击中9环以上(含9环)的概率
(3)若甲运动员射击2次,乙运动员射击1次, 表示这3次射击中击中9环以上(含9环)的次数,求
表示这3次射击中击中9环以上(含9环)的次数,求 的分布列及
的分布列及 .
.
如图,在三棱柱 中,已知
中,已知

 学,,,,,网,
学,,,,,网, 侧面
侧面 ,
,
(1)求直线C1B与底面ABC所成角正切值;
(2)在棱 (不包含端点
(不包含端点 上确定一点
上确定一点 的位置,
的位置,
使得 (要求说明理由).
(要求说明理由).
(3)在(2)的条件下,若 ,求二面角
,求二面角 的大小.
的大小.

如图,设抛物线 的准线与
的准线与 轴交于
轴交于 ,焦点为
,焦点为 ;以
;以 为焦点,离心率
为焦点,离心率 的椭圆
的椭圆 与抛物线
与抛物线 在
在 轴上方的交点为
轴上方的交点为 ,延长
,延长 交抛物线于点
交抛物线于点 ,
, 是抛物线
是抛物线 上一动点,且M在
上一动点,且M在 与
与 之间运动.
之间运动.
(1)当 时,求椭圆
时,求椭圆 的方程;
的方程;
(2)当 的边长恰好是三个连续的自然数时,求
的边长恰好是三个连续的自然数时,求 面积的最大值.
面积的最大值.
已知函数
(1)若函数 在定义域内单调递增,求
在定义域内单调递增,求 的取值范围;
的取值范围;
(2)若 且关于x的方程
且关于x的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;
(3)设各项为正的数列 满足:
满足: 求证:
求证:
(本小题满分10分)选修4—1:几何证明选讲
如图,⊙ 的直径
的直径 的延长线与弦
的延长线与弦 的延长线相交于点
的延长线相交于点 ,
,
 为⊙
为⊙ 上一点,AE=AC ,
上一点,AE=AC , 交
交 于点
于点 ,且
,且 ,
,
(1)求 的长度.
的长度.
(2)若圆F且与圆 内切,直线PT与圆F切于点T,求线段PT的长度
内切,直线PT与圆F切于点T,求线段PT的长度
(本小题满分10分)选修4—4:坐标系与参数方程
在极坐标系下,已知圆O: 和直线
和直线 ,
,
(1)求圆O和直线 的直角坐标方程;
的直角坐标方程;
(2)当 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.
 ,则
,则 ( )
( )



 所对应的点位于( )
所对应的点位于( ) ,
, ,
, ,则向量
,则向量 在向量
在向量 方向上的投影是( )
方向上的投影是( )



 的图象如下图,则( )
的图象如下图,则( )




 满足:
满足: ,若存在两项
,若存在两项 使得
使得 ,则
,则 的最小值为( )
的最小值为( )


 ______________.
______________. 
 的内角
的内角 所对的边分别为
所对的边分别为 且
且 .
. 的大小;
的大小; ,求
,求 的取值范围.
的取值范围.
 和
和 ,不等式
,不等式 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号