[湖南]2012-2013年湖南长沙高二上第一学月理科数学试卷
已知有相同两焦点 的椭圆
的椭圆 和双曲线
和双曲线 ,
, 是它们的一个交点,则
是它们的一个交点,则 的形状是 ( )
的形状是 ( )
| A.锐角三角形 | B.直角三角形 | C.钝有三角形 | D.等腰三角形 |
来源:2012-2013年湖南长沙高二上第一学月理科数学试题
若实数 满足
满足 且
且 ,则称
,则称 与
与 互补.记
互补.记 ,那么
,那么 是
是 与
与 互补的 ( ) 条件
互补的 ( ) 条件
| A.必要不充分 | B.充分而不必要 | C.充要 | D.既不充分也不必要 |
来源:2012-2013年湖南长沙高二上第一学月理科数学试题
点 在直线
在直线 上,若存在过
上,若存在过 的直线交抛物线
的直线交抛物线 于
于 两点,且
两点,且 ,则称点
,则称点 为“
为“ 点”,那么下列结论中正确的是( )
点”,那么下列结论中正确的是( )
A.直线 上的所有点都是“ 上的所有点都是“ 点” 点” |
B.直线 上仅有有限个点是“ 上仅有有限个点是“ 点” 点” |
C.直线 上的所有点都不是“ 上的所有点都不是“ 点” 点” |
D.直线 上有无穷多个点是“ 上有无穷多个点是“ 点” 点” |
来源:2012-2013年湖南长沙高二上第一学月理科数学试题
过双曲线 的右焦点F,作渐近线
的右焦点F,作渐近线 的垂线与双曲线左右两支都相交,则双曲线的离心率
的垂线与双曲线左右两支都相交,则双曲线的离心率 的取值范围为 ( )
的取值范围为 ( )
A. |
B. |
C. |
D. |
来源:2012-2013年湖南长沙高二上第一学月理科数学试题
已知点P为双曲线 右支上一点,F1、F2分别为双曲线的左、右焦点,I为
右支上一点,F1、F2分别为双曲线的左、右焦点,I为 的内心,若
的内心,若 成立,则
成立,则 的值为 ( )
的值为 ( )
A. |
B. |
C. |
D. |
来源:2012-2013年湖南长沙高二上第一学月理科数学试题
(1)已知 的图象为双曲线,在双曲线的两支上分别取点
的图象为双曲线,在双曲线的两支上分别取点 ,则线段
,则线段 的最小值为 ;
的最小值为 ;
(2)已知 的图象为双曲线,在此双曲线的两支上分别取点
的图象为双曲线,在此双曲线的两支上分别取点 ,则线段
,则线段 的最小值为 。
的最小值为 。
来源:2012-2013年湖南长沙高二上第一学月理科数学试题
给定两个命题,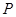 :对任意实数
:对任意实数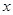 都有
都有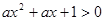 恒成立;
恒成立;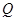 :关于
:关于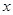 的方程
的方程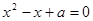 有实数根;如果“
有实数根;如果“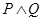 ”为假,且“
”为假,且“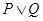 ”为真,求实数
”为真,求实数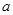 的取值范围。
的取值范围。
来源:2012-2013年湖南长沙高二上第一学月理科数学试题
已知椭圆的长轴长为 ,焦点是
,焦点是 ,点
,点 到直线
到直线 的距离为
的距离为 ,过点
,过点 且倾斜角为锐角的直线
且倾斜角为锐角的直线 与椭圆交于
与椭圆交于 两点,使得
两点,使得 .
.
(1)求椭圆的方程;(2)求直线 的方程.
的方程.
来源:2012-2013年湖南长沙高二上第一学月理科数学试题
已知直线 与双曲线
与双曲线 交于
交于 两点,
两点,
(1)若以 线段为直径的圆过坐标原点,求实数
线段为直径的圆过坐标原点,求实数 的值。
的值。
(2)是否存在这样的实数 ,使
,使 两点关于直线
两点关于直线 对称?说明理由.
对称?说明理由.
来源:2012-2013年湖南长沙高二上第一学月理科数学试题
 ”的否定为 ( )
”的否定为 ( )
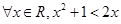

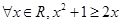
 上,横坐标为
上,横坐标为 的点到焦点的距离为
的点到焦点的距离为 ,则
,则 的值为( )
的值为( ) 的弦被点
的弦被点 平分,则此弦所在的直线方程是 ( )
平分,则此弦所在的直线方程是 ( )



 上一点
上一点 到椭圆一个焦点的距离是3,则
到椭圆一个焦点的距离是3,则 的焦点坐标是______________.
的焦点坐标是______________. 的焦点作直线
的焦点作直线 交抛物线于
交抛物线于 两点,若线段
两点,若线段 中点的横坐标为3,则
中点的横坐标为3,则 等于___________.
等于___________. 有共同的渐近线,且经过点
有共同的渐近线,且经过点 的双曲线方程是 .
的双曲线方程是 . 的端点
的端点 分别在
分别在 轴上移动,动点
轴上移动,动点 满足
满足 ,则动点
,则动点 的轨迹方程是 .
的轨迹方程是 . ,直线
,直线 的方程为
的方程为 ,在抛物线上有一动点
,在抛物线上有一动点 到
到 轴的距离为
轴的距离为 ,
, ,则
,则 的最小值为
的最小值为  的前
的前 项和
项和 ,求数列
,求数列 与抛物线
与抛物线 交于
交于 两点.
两点. 的长;(2)若抛物线
的长;(2)若抛物线 ,求
,求 的值.
的值. 的中心在原点,焦点在
的中心在原点,焦点在 轴上,短轴的一个端点与左右焦点
轴上,短轴的一个端点与左右焦点 、
、 组成一个正三角形,焦点到椭圆上的点的最短距离为
组成一个正三角形,焦点到椭圆上的点的最短距离为 .
. 与椭圆
与椭圆 、
、 两点,线段
两点,线段 的中点为
的中点为 ,求直线
,求直线 的斜率
的斜率 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号