[山东]2013届山东省济宁地区九年级第一学期期末考试数学试卷
抛物线y=x2-2x-3的顶点坐标是
| A.(1,-4) | B.(2,-4) | C.(-1,4) | D.(-2,-3) |
如果关于x的方程x2-2x+k=0有两个相等的实数根,那么k的值等于
| A.1 | B.2 | C.0 | D.-1 |
若两圆的半径分别为2cm,3cm,圆心距是6cm,那么这两圆的位置关系是
| A.外切 | B.内切 | C.内含 | D.外离 |
若△ABC∽△DEF,相似比为1︰2,△ABC的面积是3cm2,则△DEF的面积是
| A.3cm2 | B.6cm2 | C.12cm2 | D.2cm2 |
如图,D,E分别是△ABC的边AB,AC上的点,且DE∥BC,如果AD=2cm,DB=4cm,△ADE的周长是10cm,那么△ABC的周长等于
| A.15cm | B.20cm | C.30cm | D.36cm |
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径是2 cm,则弦CD的长为
cm,则弦CD的长为
A.2 cm cm |
B.6cm | C.3cm | D. cm cm |
抛物线y=ax2+bx+c的顶点坐标是(-1,3),且过点(0,5),那么二次函数y=ax2+bx+c的解析式为
| A.y=-2x2+4x+5 | B.y=2x2+4x+5 |
| C.y=-2x2+4x-1 | D.y=2x2+4x+3 |
一个暗箱里装有10个黑球,6个白球,14个红球,搅匀后随机摸出一个球,则摸到白球的概率是
A. |
B. |
C. |
D. |
用一根长为24cm的铁丝围成一个矩形,如果矩形的面积是35 cm2,那么这个矩形的长与宽分别是
| A.7 cm,5 cm | B.8 cm,4 cm |
| C.9 cm,3 cm | D.6 cm,6 cm |
将抛物线y=x2向左平移1个单位,再向下平移2个单位,得到抛物线的解析式为
| A.y=x2-2x-1 | B.y=-x2+2x-1 |
| C.y=x2+2x-1 | D.y=-x2+4x+1 |
二次函数y=ax2+bx+c的图象如图所示,则下列结论错误的是
| A.abc>0 | B.a-b+c=0 |
| C.a+b+c>0 | D.4a-2b+c>0 |
如图,BC为半圆O的直径,CA为切线,AB交半圆O于点E,EF⊥BC于点F,连接EC.则图中与△CEF相似的三角形共有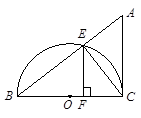
A. 1个 B.2个 C.3个 D.4个
如图,把⊙O1向右平移8个单位长度得⊙O2,两圆相交于A,B,且O1A⊥O2A,则图中阴影部分的面积是_____ ______.
(1)用因式分解法解方程 x(x+1) =2(x+1) .
(2)已知二次函数的解析式为y=x2-4x-5,请你判断此二次函数的图象与x轴交点的个数;并指出当y随x的增大而增大时自变量x的取值范围.
如图,九(1)班同学到野外上数学活动课,为测量一条河的宽度,先在河的一岸平地上取一条线段BC,点A在河的对岸,AB⊥BC;在线段BC上选取一点D,以CD为一条直角边构造Rt△ECD,使点E在直线AD上.经测量BD=120m,DC=60m, EC=50m,请你帮助九(1)班同学求出河宽AB.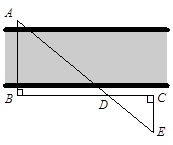
一个不透明的布袋里装有4个大小、质地均相同的乒乓球,每个球上面分别标有1,2,3,4.小林先从布袋中随机抽取一个乒乓球(不放回去),再从剩下的3个球中随机抽取第二个乒乓球.
(1)请你列出所有可能的结果;
(2)求两次取得乒乓球的数字之积为奇数的概率.
如图,点D、E分别是△ABC的边AC、AB上的点,AC·AD=AB·AE.
(1)△ADE与△ABC相似吗?请你说明理由;
(2)若AD=3,AB=6,DE=4,求BC的长.
某企业2007年盈利1500万元,2009年克服全球金融危机的不利影响,仍实现盈利2160万元.从2007年到2009年,如果该企业每年盈利的年增长率相同.
(1)求该企业2008年盈利多少万元?
(2)若该企业盈利的年增长率继续保持不变,预计2010年盈利多少万元?
如图,直线y=2x-2与x轴交于点A,抛物线y=ax2+bx+c的对称轴是直线x=3,抛物线经过点A,且顶点P在直线y=2x-2上.
(1)求A、P两点的坐标及抛物线y=ax2+bx+c的解析式;
(2)画出抛物线的草图,并观察图象写出不等式ax2+bx+c>0的解集.
如图,AB是⊙O的直径,CB、CD是⊙O的两条切线,D为切点,AC与⊙O交于点E,连接BE.
(1)求证:△BEC∽△ABC;
(2)若CE=4,AE=5,求切线CD的长.
 ×
× = .
= . 有意义的自变量x的取值范围是 .
有意义的自变量x的取值范围是 .

 粤公网安备 44130202000953号
粤公网安备 44130202000953号