江苏省大丰市初一第一学期末数学卷
如图,长方形OABC中,O为平面直角坐标系的原点,A、C两点的坐标分别为(3,0),(0,5),点B在第一象限 内
内



(1) 如图1,写出点B的坐标.
(2)如图2,若过点C的直线CD交AB于点D,且把长方形OABC的周长分为3:1两部分,求点D坐标;
(3)如图3,将(2)中的线段CD向下平移2个单位,得到C/D/,试计算四边形OAD/C/面积
如图,⊙O的半径为1,点P是⊙O上一点,弦AB垂直平分线段OP,点D是 上任一点(与端点A、B不重合),DE⊥AB于点E,以点D为圆心、DE长为半径作⊙D,分别过点A、B作⊙D的切线,两条切线相交于点C.
上任一点(与端点A、B不重合),DE⊥AB于点E,以点D为圆心、DE长为半径作⊙D,分别过点A、B作⊙D的切线,两条切线相交于点C.
(1)求弦AB的长;
(2)判断∠ACB是否为定值,若是,求出∠ACB的大小;否则,请说明理由;
(3)记△ABC的面积为S,若 =4
=4 ,求△ABC的周长.
,求△ABC的周长.
工地调来72人参加挖土和运土,已知3人挖出的土1人恰好能全部运走,怎样调动劳动力才能使挖出的土 能及时运走,解决此问题,可设派x人挖土,其它的人运土,列方程①
能及时运走,解决此问题,可设派x人挖土,其它的人运土,列方程①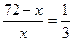 ②72-x=
②72-x=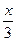 ③x+3x="72" ④
③x+3x="72" ④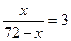
 上述所列方程,正确的有( )个
上述所列方程,正确的有( )个
A 1 B 2 C 3 D 4
把分式方程 ,的两边同时乘以x-2,约去分母,得( )
,的两边同时乘以x-2,约去分母,得( )
A 1-(1-x )="1 " B 1+(1-x)="1 " c 1-(1-x)="x-2 " D 1+(1-x)=x-2
)="1 " B 1+(1-x)="1 " c 1-(1-x)="x-2 " D 1+(1-x)=x-2
张老师和李老师同时从学校出发,步行15千米去县城购买书籍,张老师比李老师每小时多走1千米,结果比李老师早到半小时,两位老师每小时各走多少 千米?设李老师每小时走x千米,依题意,得到的方程是:( )
千米?设李老师每小时走x千米,依题意,得到的方程是:( )
A. |
B. |
C. ( ( |
D. |
如图,AB⊥AC,AD⊥BC,那么点C到直线AD的距离是指 ( )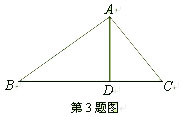
| A.线段AC的长 | B.线段AD的长 | C.线段DB的长 | D.线段CD的长 |
如图,点O在直线AB上,且OC⊥OD,若∠COA=36°,则∠DOB的大小为( ▲ )
| A.36° | B.54° | C.64° | D.72° |
如图所示,由M观测N的方向是 ( ▲ )
| A.北偏西60° | B.南偏东60° | C.北偏西30° | D.南偏东30° |
一队师生共328人,乘车外出旅行,已有校车可乘64人,如果租用客车,每辆可乘44人,那么还要租用多少辆客车?在这个问题中,如果还要租 辆客车,可列方程为( ▲ )
辆客车,可列方程为( ▲ )
A. |
B. |
C. |
D. |
观察下图及图形所对应的算式,根据你发现的规律计算1+8+16+24+……+8n(n是正整数)的结果为 ( ▲ )
A. |
B. |
C. |
D. |
一张桌子上重叠摆放了若干枚面值一元的硬币,从三个不同方向看它得到的平面图形如上图所示,那么桌上共有 ▲ 枚硬币.
计算(每小题4分,共16分)
(1)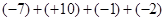
(2)-22×5-(-3)×-5÷(-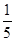 )
)
(3)4x2y-9xy2+7-4x2y+10xy2-4
(4)3(2x2-xy)-4(x2-xy+3)
画图题.利用网络线画图.过点P画直线AB的平行线PQ,画PM⊥AB
垂足为C.(要在图中标出相关的点保留画图痕迹)(6分)
“ ”是新规定的这样一种运算法则:
”是新规定的这样一种运算法则: ,比如
,比如 (8分)
(8分)
(1)试求 的值;
的值;
(2)若 ,求
,求 的值;
的值;
(3)若(-2) =
= +9,求
+9,求 的值
的值
段AB=12 cm,点O是线段AB中点,点C是线段AB上一点,且AC= BC,
BC,
P是线段AC的中点.(8分)
(1)求线段OP的长.(如图所示)
(2)若将题目中:点C是线段AB上一点,改为点C是直线AB上一点,线段OP还可以是多长?(画出示意图)
剃须刀由刀片和刀架组成。某时期,甲、乙两厂家分别生产老式剃须刀(刀片不可更换)和新式剃须刀(刀片可更换),有关销售策略与售价等信息如下表所示:
某段时间内,甲厂家销售了8000把剃须刀,乙厂家销售的刀片数量是刀架数量的50倍,乙厂家获得的利润是甲的两倍,问这段时间内,乙销售了多少把刀架?多少片刀片?(10分)
| |
老式剃须刀 |
新式剃须刀 |
|
| 刀架 |
刀片 |
||
| 售价 |
2.5(元/把) |
1 (元/把) |
0.55(元/片) |
| 成本 |
2 (元/把) |
6 (元/把) |
0.05(元/片) |
如图,已知OE平分∠AOC,OF平分∠BOC (12分)
(1)若∠AOB是直角,∠BOC=60°,求∠EOF的度数。
(2)若∠AOC=x°,∠EOF=y°,∠BOC=60°,请用x 的代数式来表示y.
(3)如果∠AOC+∠EOF=210°,∠BOC=60°,则∠EOF是多少度?
我们常用的数是十进制数,计算机程序使用的是二进制数(只有数码0和1),它们两者之间可以互相换算,如将(101) ,(1011)
,(1011)  换算成十进制数为:
换算成十进制数为:
(101)  =1×2
=1×2 +0×2
+0×2 +1=4+0+1=5;(1011)
+1=4+0+1=5;(1011)  =1×2
=1×2 +0×2
+0×2 +1×2
+1×2 +1=11;
+1=11;
两个二进制数可以相加减,相加减时,将对应数位上的数相加减.与十进制中的“逢十进一”、“退一还十”相类似,应用“逢二进一”、“退一还二”的运算法则,如: (101)  +(11)
+(11)  ="(1000)"
="(1000)"  ;(110)
;(110)  +(11)
+(11)  ="(11)"
="(11)"  ,用竖式运算如右侧所示.(12分)
,用竖式运算如右侧所示.(12分)
(1)按此方式,将二进制(1001)2换算成十进制数的结果是 ▲ .
(2)计算:(10101)  +(111)
+(111)  = ▲ (结果仍用二进制数表示);
= ▲ (结果仍用二进制数表示);
(110010)  -(1111)
-(1111)  = ▲ (结果用十进制数表示).
= ▲ (结果用十进制数表示).



 C (-2m-n)2=4m-n D (a+b)-1=a-1+b-1
C (-2m-n)2=4m-n D (a+b)-1=a-1+b-1 的最简公分母是( )
的最简公分母是( ) -0.00036 D -36000
-0.00036 D -36000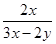 中的x,y都扩大3倍,那么分式的值( )
中的x,y都扩大3倍,那么分式的值( )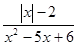 的值为0,则x的值为( )
的值为0,则x的值为( ) 的结果是( )
的结果是( ) D
D 
 中,分式的个数是( )
中,分式的个数是( ) ( ).
( ). 的值是( )
的值是( )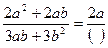
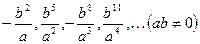 ,其中第7个式子是 第n个式子是
,其中第7个式子是 第n个式子是  =" "
=" " 的解是
的解是  =" "
=" "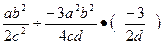
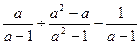
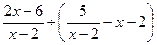
 的值
的值  ,求
,求 的值
的值 ,然后取一组m,n的值代入求值
,然后取一组m,n的值代入求值

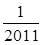
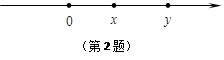
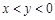
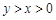
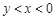
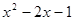 的值等于4,则代数式
的值等于4,则代数式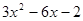 的值 ( ▲ )
的值 ( ▲ ) 的解为___________▲______
的解为___________▲______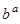 = ▲
= ▲  的值= ▲
的值= ▲



 a2+8a-
a2+8a- -6a-
-6a- a2+
a2+ ,其中a=
,其中a=
 ,其中
,其中 

 粤公网安备 44130202000953号
粤公网安备 44130202000953号