[浙江]2013届浙江省五校联盟高三下学期第一次联考理科数学试卷
复数 ,则复数
,则复数 在复平面内对应的点位于 ( )
在复平面内对应的点位于 ( )
| A.第一象限 | B.第二象限 |
| C.第三象限 | D.第四象限 |
已知 ,则“
,则“ ”是“
”是“ 恒成立”的( )
恒成立”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知两个不重合的平面 ,给定以下条件:
,给定以下条件:
① 内不共线的三点到
内不共线的三点到 的距离相等;②
的距离相等;② 是
是 内的两条直线,且
内的两条直线,且 ;
;
③ 是两条异面直线,且
是两条异面直线,且 ;
;
其中可以判定 的是( )
的是( )
| A.① | B.② | C.①③ | D.③ |
在平面直角坐标系中,不等式
 为常数
为常数 表示的平面区域的面积为8,则
表示的平面区域的面积为8,则 的最小值为( )
的最小值为( )
A. |
B. |
C. |
D. |
已知P为抛物线 上一个动点,Q为圆
上一个动点,Q为圆 上一个动点,那么点P到点Q的距离与点P到
上一个动点,那么点P到点Q的距离与点P到 轴距离之和最小值是( )
轴距离之和最小值是( )
A.  |
B.  |
C. |
D.  |
将一个三位数的三个数字顺序颠倒,将所得到的数和原数相加,若和中没有一个数字是偶数,则称这个数是奇和数。那么,所有的三位数中,奇和数有( )
| A.80 | B.100 | C.120 | D.160 |
公比为4的等比数列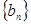 中,若
中,若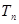 是数列
是数列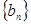 的前
的前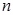 项积,则有
项积,则有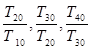 也成等比数列,且公比为
也成等比数列,且公比为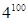 ;类比上述结论,相应的在公差为3的等差数列
;类比上述结论,相应的在公差为3的等差数列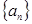 中,若
中,若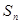 是
是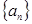 的前
的前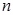 项和,则有一相应的等差数列,该等差数列的公差为________ ______.
项和,则有一相应的等差数列,该等差数列的公差为________ ______.
有一种游戏规则如下:口袋里有5个红球和5个黄球,一次摸出5个,若颜色相同则得100分,若4个球颜色相同,另一个不同,则得50分,其他情况不得分。小张摸一次得分的期望是分__ _ _ ______.
设双曲线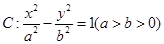 的右焦点为
的右焦点为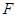 ,左右顶点分别为
,左右顶点分别为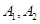 ,过
,过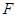 且与双曲线
且与双曲线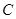 的一条渐近线平行的直线
的一条渐近线平行的直线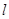 与另一条渐近线相交于
与另一条渐近线相交于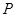 ,若
,若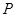 恰好在以
恰好在以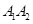 为直径的圆上,则双曲线的离心率为________ ______.
为直径的圆上,则双曲线的离心率为________ ______.
已知三个正整数 按某种顺序排列成等差数列。
按某种顺序排列成等差数列。
(1)求 的值;
的值;
(2)若等差数列 的首项、公差都为
的首项、公差都为 ,等比数列
,等比数列 的首项、公比也都为
的首项、公比也都为 ,前
,前 项和分别为
项和分别为 ,且
,且 ,求满足条件的正整数
,求满足条件的正整数 的最大值。
的最大值。
(本小题满分14分)
在四棱锥 中,
中, //
// ,
, ,
,  ,
, 平面
平面 ,
, .
. 
(Ⅰ)设平面 平面
平面 ,求证:
,求证: //
// ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)设点 为线段
为线段 上一点,且直线
上一点,且直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值.
的值.
椭圆 :
: 的右焦点
的右焦点 与抛物线
与抛物线 的焦点重合,过
的焦点重合,过 作与
作与 轴垂直的直线
轴垂直的直线 与椭圆交于
与椭圆交于 两点,与抛物线交于
两点,与抛物线交于 两点,且
两点,且 。
。
(1)求椭圆 的方程;
的方程;
(2)若过点 的直线与椭圆
的直线与椭圆 相交于两点
相交于两点 ,设
,设 为椭圆
为椭圆 上一点,且满足
上一点,且满足
 为坐标原点),当
为坐标原点),当 时,求实数
时,求实数 的取值范围。
的取值范围。
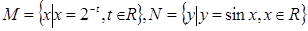 ,则
,则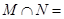 ( )
( )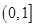
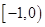
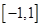
 的值是( )
的值是( )
 对任意实数
对任意实数 都有
都有 ,则
,则 的值等于( )
的值等于( )


 的零点个数判断正确的是 )
的零点个数判断正确的是 ) 的展开式中的常数项为___ __.
的展开式中的常数项为___ __.
 ,则
,则
 _ _.
_ _. 是锐角
是锐角 的外接圆的圆心,且
的外接圆的圆心,且 ,若
,若 ,则
,则 =________ ______.
=________ ______. 中,
中, 分别是内角
分别是内角 所对边长,且满足
所对边长,且满足 。
。 的大小;
的大小; ,求
,求

 为常数,
为常数,
 时,求函数
时,求函数 在
在 处的切线方程;
处的切线方程;  在
在 处取得极值时,若关于
处取得极值时,若关于 的方程
的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围; ,总存在
,总存在 ,使不等式
,使不等式 成立,求实数
成立,求实数 的取值范围。
的取值范围。 粤公网安备 44130202000953号
粤公网安备 44130202000953号