[浙江]2012-2013学年浙江省杭州地区七校高二期中联考数学试卷

直线的倾斜角是(       )

利用斜二测画法可以得到：
①三角形的直观图是三角形；②平行四边形的直观图是平行四边形；
③正方形的直观图是正方形；④菱形的直观图是菱形． 以上结论正确的是(      )

若直线3x＋y＋a＝0过圆x²＋y²＋2x－4y＝0的圆心，则a的值为(      )

设α，β为不重合的平面，m，n为不重合的直线，则下列命题正确的是(      )

A．若mα，nβ，m∥n，则α∥β

B．若n⊥α，n⊥β，m⊥β，则m⊥α

C．若m∥α，n∥β，m⊥n，则α⊥β

D．若α⊥β，n⊥β，m⊥n，则m⊥α

在三棱锥P-ABC中，若PA=PB=PC,则顶点P在底面ABC上的射影O必为△ABC的(    )

直线y＝kx＋3与圆(x－2)²＋(y－3)²＝4相交于M、N两点，若|MN|≥2，则直线倾斜角的取值范围是(      )

A．	B．
C．	D．

△一边BC在平面内,顶点A在平面外,已知，三角形所在平面与所成的二面角为,则直线与所成角的正弦值为(      )

A．

B．

C．

D．

已知点P在直线x＋3y－1＝0上，点Q在直线x＋3y＋3＝0上，PQ中点为M(x₀，y₀)，
且y₀≥x₀＋2，则的取值范围为(      )

A．	B．
C．	D．

如图，在正方体中，点在线段上移动，则异面直线与所成的角的取值范围(      )

A．	B．
C．	D．

已知直线和圆，圆心为M,点在直线上，若圆与直线至少有一个公共点，且，则点的横坐标的取值范围是(    )

A．

B．

C．

D．

在空间直角坐标系O-xyz中，若A(1,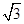,2)关于y轴的对称点为A₁，则线段AA₁的长度为      

圆x²+y²=20的弦AB的中点为P(2,-3)，则弦AB所在直线的方程是                 

如右图，某几何体的正视图是平行四边形，侧视图和俯视图都是矩形，则该几何体的体积为                  

如下图所示，将平面四边形ABCD折成空间四边形，当平面四边形满足条件                      时，空间四边形中的两条对角线互相垂直（填一个正确答案就可以，不必考虑所有可能情形）

已知直线与轴分别交于点，为坐标原点，则点到平分线的距离为                   

过圆C：作一动直线交圆C于两点A、B，过坐标原点O作直线ON⊥AM于点N，过点A的切线交直线ON于点Q，则=      （用R表示）

如图所示的三棱锥A-BCD中，∠BAD=90°，AD⊥BC，AD=4，AB=AC=2，∠BAC=120°，若点P为△ABC内的动点满足直线DP与平面ABC所成角的正切值为2，则点P在△ABC内所成的轨迹的长度为              

已知点、到直线的距离相等，且直线经过两条直线和的交点，求直线的方程。

如图，在四棱锥中，底面ABCD是一直角梯形，，,，且PA=AD=DC=AB=1.

(1)证明：平面平面
(2)设AB,PA,BC的中点依次为M、N、T，求证：PB∥平面MNT
(3)求异面直线与所成角的余弦值

如图，⊥平面，=90°，，点在上，点E在BC上的射影为F,且．

（1）求证：；
（2）若二面角的大小为45°，求的值．

已知圆的方程为，过点作直线与圆交于、两点。

(1)若坐标原点O到直线AB的距离为，求直线AB的方程；
(2)当△的面积最大时，求直线AB的斜率；
(3)如图所示过点作两条直线与圆O分别交于R、S,若，且两角均为正角，试问直线RS的斜率是否为定值，并说明理由。