[江苏]2005年初中毕业升学考试(江苏淮安卷)数学
下列计算中,正确的是
| A.a10÷a5=a2 | B.3a-2a=a | C.a3-a3=1 | D.(a2)3=a5 |
截至今年一季度末,江苏省企业养老保险参保人数达850万,则参保人数用科学记数法表示为
| A.8.50×106 | B.8.50×105 | C.0.850×106 | D.8.50×107 |
如图,直线a∥b,直线c是截线,如果∠1=50°,那么∠2等于
| A.150° | B.140° | C.130° | D.120° |
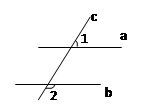
关于x的一元二次方程x2-x+ m=0有两个不相等的实数根,则实数m的取值范围是
m=0有两个不相等的实数根,则实数m的取值范围是
| A.m<1 | B.m<-1 | C.m≤1 | D.m>1 |
如图,PAB、PCD为⊙O的两条割线,AD、BC相交于点E,则图中相似三角形共有
A.0对 B.1对 C.2对 D.3对
S型电视机经过连续两次降价,每台售价由原来的1500元降到了980元.设平均每次降价的百分率为x,则下列方程中正确的是
| A.1500 (1+x)2=980 | B.980(1+x)2=1500 |
| C.1500 (1-x)2=980 | D.980(1-x)2="1500" |
如果三角形的两边长为2和9,且周长为奇数,那么满足条件的三角形共有
| A.1个 | B.2个 | C.3个 | D.4个 |
如果点O为△ABC的外心,∠BOC=70°,那么∠BAC等于
| A.35° | B.110° | C.145° | D.35°或145° |
用换元法解方程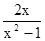 -
-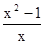 =1,如果设
=1,如果设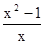 =y,那么原方程可转化为
=y,那么原方程可转化为
| A.2y2-y-1=0 | B.2y2+y-1=0 |
| C.y2+y-2=0 | D.y2-y+2=0 |
一只封闭的圆柱形水桶(桶的厚度忽略不计),底面直径为20cm,母线长为40cm,盛了半桶水,现将该水桶水平放置后如图所示,则水所形成的几何体的表面积为
| A.800 cm2 | B.(800+400π) cm2 |
| C.(800+500π)cm2 | D.(1600+1200π)cm2 |
已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成下列形式:
第1行 1
第2行 -2 3
第3行 -4 5 -6
第4行 7 -8 9 -10
第5行 11 -12 13 -14 15
… …
按照上述规律排下去,那么第10行从左边数第5个数等于
| A.50 | B.-50 | C.60 | D.-60 |
三明中学初三(1)班篮球队有10名队员,在一次投篮训练中,这10名队员各投篮50次的进球情况如下表:
| 进球数 |
42 |
32 |
26 |
20 |
19 |
18 |
15 |
14 |
| 人数 |
1 |
1 |
1 |
1 |
2 |
1 |
2 |
1 |
针对这次训练,请解答下列问题:
(1)求这10名队员进球数的平均数、中位数和众数;
(2)求这支球队整体投篮命中率;(投篮命中率= ×100%)
×100%)
(3)若队员小华的投篮命中率为40%,请你分析一下小华在这支球队中的投篮水平.
如图,在一张圆桌(圆心为点O)的正上方点A处吊着一盏照明灯,实践证明:桌子边沿处的光的亮度与灯距离桌面的高度AO有关,且当sin∠ABO= 时,桌子边沿处点B的光的亮度最大,设OB=60cm,求此时灯距离桌面的高度OA(结果精确到1cm).
时,桌子边沿处点B的光的亮度最大,设OB=60cm,求此时灯距离桌面的高度OA(结果精确到1cm).
(参考数据: ≈1.414;
≈1.414; ≈1.732;
≈1.732; ≈2.236)
≈2.236)
已知: ABCD的对角线交点为O,点E、F分别在边AB、CD上,分别沿DE、BF折叠四边形ABCD, A、C两点恰好都落在O点处,且四边形DEBF为菱形(如图).
ABCD的对角线交点为O,点E、F分别在边AB、CD上,分别沿DE、BF折叠四边形ABCD, A、C两点恰好都落在O点处,且四边形DEBF为菱形(如图).
⑴求证:四边形ABCD是矩形;
⑵在四边形ABCD中,求 的值.
的值.
已知抛物线y=ax2+bx+c过点A(0,2)、B(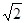 ,
,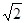 ),且点B关于原点的对称点C也在该抛物线上.
),且点B关于原点的对称点C也在该抛物线上.
⑴求a、b、c的值;
⑵①这条抛物线上纵坐标为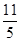 的点共有 个;
的点共有 个;
②请写出: 函数值y随着x的增大而增大的x的一个范围 .
如图,AB是⊙O的直径,点C在BA的延长线上,CA=AO,点D在⊙O上,∠ABD=30°.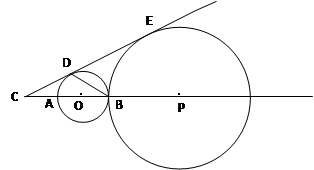
⑴求证:CD是⊙O的切线;
⑵若点P在直线AB上,⊙P与⊙O外切于点B,与直线CD相切于点E,设⊙O与⊙P的半径分别为r与R,求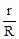 的值.
的值.
联想中学本学期前三周每周都组织初三年级学生进行一次体育活动,全年级400名学生每人每次都只参加球类或田径类中一个项目的活动.假设每次参加球类活动的学生中,下次将有20%改为参加田径类活动;同时每次参加田径类活动的学生中,下次将有30%改为参加球类活动.
⑴如果第一次与第二次参加球类活动的学生人数相等,那么第一次参加球类活动的学生应有多少名?
⑵如果第三次参加球类活动的学生不少于200名,那么第一次参加球类活动的学生最少有多少名?
 的图象上的是
的图象上的是 ,3)
,3) 的自变量x的取值范围是
的自变量x的取值范围是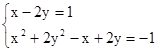 的实数解个数为
的实数解个数为 )-1 = .
)-1 = . 的值等于 .
的值等于 .
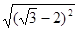 -
-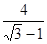 .
. )÷
)÷ .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号