[江苏]2005年初中毕业升学考试(江苏苏州卷)数学
右图可以看作是一个等腰直角三角形旋转若干次而生成的则每次旋转的度数可以是
| A.900 | B.600 |
| C.450 | D.300 |
苏州红十字会统计,2004年苏州是无偿鲜血者总量为12.4万人次,已连续6年保持全省第一。12.4万这个数用科学记数法来表示是
| A.1.24×104 | B.1.24×105 | C.1.24×106 | D.12.4×104 |
将直线y=2x向上平移两个单位,所得的直线是
| A.y=2x+2 | B.y=2x-2 | C.y=2(x-2) | D.y=2(x+2) |
初二(1)班有48位学生,春游前,班长把全班学生对春游地点的意向绘制成了扇形统计图,其中“想去苏州乐园的学生数”的扇形圆心角600,则下列说法正确的是
| A.想去苏州乐园的学生占全班学生的60% |
| B.想去苏州乐园的学生有12人 |
| C.想去苏州乐园的学生肯定最多 |
| D.想去苏州乐园的学生占全班学生的1/6 |
如图,已知等腰梯形ABCD的中位线EF的长为6,腰AD的长为5,则该等腰梯形的周长为
| A.11 | B.16 | C.17 | D.22 |
如图的转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等,四位同学各自发表了下述见解:
甲:如果指针前三次都停在了3号扇形,下次就一定不会停在3号扇形了
乙:只要指针连续转六次,一定会有一次停在6号扇形
丙:指针停在奇数号扇形的概率和停在偶数号扇形的概率相等
丁:运气好的时候,只要在转动前默默想好让指针停在6号扇形,指针停在6号扇形的可能性就会加大。
其中你认为正确的见解有
| A.1个 | B.2个 | C.3个 | D.4个 |
温家宝总理有句名言:“多么小的问题乘以13亿,都会变得很大;多么大的经济总量,除以13亿都会变得很小”据国家统计局的公布,2004年我国淡水资源总量为26520亿立方米,居世界第四位,但人均只有 立方米,是全球人均水资源最贫乏的十三个国家之一。
下表给出了苏州市2005年5月28日至6月3日的最高气温,则这些最高气温的极差是 ℃。
| 日 期 |
5月28日 |
5月29日 |
5月30日 |
5月31日 |
6月1日 |
6月2日 |
6月3日 |
| 最高气温 |
26℃ |
27℃ |
30℃ |
28℃ |
27℃ |
29℃ |
33℃ |
如图,平行四边形纸条ABCD中,E,F分别是边AD,BC的中点,张老师请同学将纸条的下半部分 沿EF翻折,得到一个V字形图案。
沿EF翻折,得到一个V字形图案。
(1)请你在原图中画出翻折后的图形 ;(用尺规作图,不写画法,保留作图痕迹)
;(用尺规作图,不写画法,保留作图痕迹)
(2)已知∠A=630,求∠B′FC的大小。
如图,小明,小华用四张扑克牌玩游戏,他俩将扑克牌洗均匀后,背面朝上放置在桌面上,小明先抽,小华后抽,抽出的牌不放回。
(1)若小明恰好抽到的黑桃4。
①请在右边筐中绘制这种情况的树状图;
②求小华抽出的牌的牌面数字比4大的概率。
(2)小明、小华约定:若小明抽到的牌的牌面数字比小华的大,则小明胜;反之,则小明负,你认为这个游戏是否公平?说明你的理由。
如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD//CO。
(1)求证:△ADB∽△OBC;
(2)若AB=2,BC= ,求AD的长。(结果保留根号)
,求AD的长。(结果保留根号)
为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,为标明限高,请你根据该图计算CE。(精确到0.1m)
已知二次函数 。
。
(1)求证:对于任意实数m,该二次函数图象与x轴总有公共点;
(2)若该二次函数图象与x轴有两个公共点A,B,且A点坐标为(1,0),求B点坐标。
苏州市区某居民小区有800户人家,有关部门准备对该小区的自来水管网系统进行改造,为此,需了解该小区的自来水用水情况。该部门通过随机抽样,调查了其中30户家庭,已知这39户家庭共有87人。
(1)这30户家庭平均每户 人。(精确到0.1人)
(2)这30户家庭的月用水量见下表:
求这30户的人均日用水量;(一个月按30天计算,精确到0.001m3)
(3)根据上述数据,试估计该小区的日用水量?(精确到1m3)
(1)如图一,等边△ABC中,D是AB上的动点,以CD为一边,向上作等边△EDC,连结AE。求证:AE//BC;
(2)如图二,将(1)中等边△ABC的形状改成以BC为底边的等腰三角形。所作△EDC改成相似于△ABC。请问:是否仍有AE//BC?证明你的结论。

苏州地处太湖之滨,有丰富的水产养殖资源,水产养殖户李大爷准备进行大闸蟹与河虾的混合养殖,他了解到如下信息:
①每亩水面的年租金为500元,水面需按整数亩出租;
②每亩水面可在年初混合投放4公斤蟹苗和20公斤虾苗;
③每公斤蟹苗的价格为75元,其饲养费用为525元,当年可获1400元收益;
④每公斤虾苗的价格为15元,其饲养费用为85元,当年可获160元收益;
(1)若租用水面n亩,则年租金共需 元;
(2)水产养殖的成本包括水面年租金、苗种费用和饲养费用,求每亩水面蟹虾混合养殖的年利润(利润:收益—成本);
(3)李大爷现有资金25000元,他准备再向银行贷不超过25000元的款。用于蟹虾混合养殖。已知银行贷款的年利率为8%,试问李大爷应该租多少亩水面,并向银行贷款多少元.可使年利润超过35000元?
如图一,平面直角坐标系中有一张矩形纸片OABC,O为坐标原点,A点坐标为(10,0),C点坐标为(0,6),D是BC边上的动点(与点B,C不重合),现将△COD沿OD翻折,得到△FOD;再在AB边上选取适当的点E,将△BDE沿DE翻折,得到△GDE,并使直线DG、DF重合。
(1)如图二,若翻折后点F落在OA边上,求直线DE的函数关系式;
(2)设D(a,6),E(10,b),求b关于a的函数关系式,并求b的最小值;
(3)一般地,请你猜想直线DE与抛物线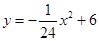 的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线
的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线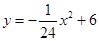 始终有公共点,请在图一中作出这样的公共点。
始终有公共点,请在图一中作出这样的公共点。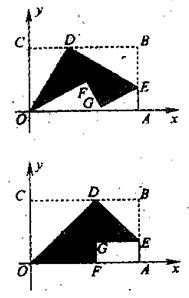









 的相反数是 。
的相反数是 。
 中自变量x的取值范围是 。
中自变量x的取值范围是 。
 ,其图象在第一、第三象限内,则k的值可为 。(写出满足条件的一个k的值即可)
,其图象在第一、第三象限内,则k的值可为 。(写出满足条件的一个k的值即可)



 粤公网安备 44130202000953号
粤公网安备 44130202000953号