[福建]2011-2012年福建省泉州市永春县八年级上册期中考试数学试卷
以线段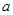 、
、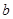 、
、 为三边的三角形是直角三角形的是( )
为三边的三角形是直角三角形的是( )
A.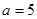 , ,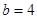 , ,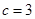 ; ; |
B. , ,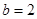 , ,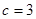 ; ; |
C.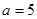 , ,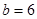 , ,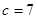 ; ; |
D.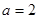 , ,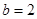 , ,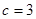 . . |
如图,矩形OABC的边OA长为2 ,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是 ( )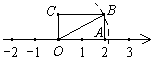
| A.2.5; | B.2 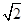 ; ; |
C.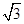 ; ; |
D.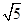 . . |
已知三角形三边的长为 、
、 、
、 ,则代数式
,则代数式 的值为( )
的值为( )
| A.正数; | B.负数; | C.0 ; | D.非负数. |
如图是矩形ABCD折叠的情况,将△ADE沿AE折叠后,点D正好落在BC边上的F处,已知AB=8,AD=10.则△AEF的面积是 .
阅读下列方法:为了找出一组数3、8、15、24、35、48、…的规律,我们用一种“因式分解法”解决这个问题.如下表:
| 项 |
1 |
2 |
3 |
4 |
5 |
6 |
… |
n |
| 值 |
3 |
8 |
15 |
24 |
35 |
48 |
… |
|
分解因式: 1×3 1×8 1×15 1×24 1×35 1×48
2×4 3×5 2×12 5×7 2×24
3×8 3×16
4×6 4×12
6×8
因此,我们得到第100项是100×102 .
请你利用上述方法,求出序列:0、5、12、21、32、45、……的第100项是 .
地球的质量约为5.98×10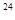 千克,木星的质量约为1.9×10
千克,木星的质量约为1.9×10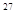 千克.问木星的质量约是地球的多少倍?(结果保留三个有效数字)
千克.问木星的质量约是地球的多少倍?(结果保留三个有效数字)
请举例说明:
① 存在两个不同的无理数, 它们的积是整数;
② 存在两个不同的无理数, 它们的差是有理数;
③ 存在两个不同的无理数, 它们的商是无理数.
如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.小明认为蚂蚁能够最快到达目的地的路径AC1,小王认为蚂蚁能够最快到达目的地的路径AC1′.已知AB=4,BC=4,CC1=5时,请你帮忙他们求出蚂蚁爬过的最短路径的长.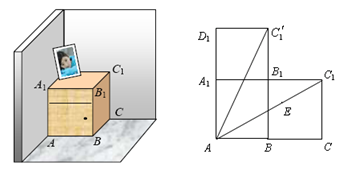
图1是一个长为2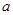 ,宽为2
,宽为2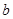 的长方形,沿图中虚线剪开,可分成四块小长方形.
的长方形,沿图中虚线剪开,可分成四块小长方形.
(1)求出图1的长方形面积;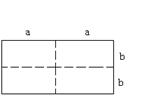
(2)将四块小长方形拼成一个图2的正方形.利用阴影部分面积的不同表示方法,直接写出代数式(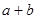 )2、(
)2、(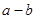 )2、
)2、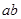 之间的等量关系;
之间的等量关系;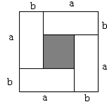
(3)把四块小长方形不重叠地放在一个长方形的内部(如图3),未被覆盖的部分用
阴影表示.求两块阴影部分的周长和(用含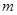 、
、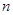 的代数式表示).
的代数式表示).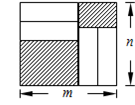
如图,已知在△ABC中,∠ACB=90°,CD⊥AB,D为垂足.
(1)若AC=8,BC=6求AB和AD的长;
(2)设AB= ,CD=
,CD= ,AC=
,AC= ,BC=
,BC= ,试说明:
,试说明: >
> .
.

 ;
;  ;
; ;
; .
.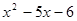 的结果为( )
的结果为( )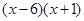 ;
;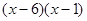 ;
;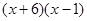 ;
; .
. 的结果是( )
的结果是( ) ;
; ;
; ;
; .
. .
. .
. 2(填“>”、“<”或“=”号).
2(填“>”、“<”或“=”号). .
. 次运算,它工作了2×102秒可作 次运算.
次运算,它工作了2×102秒可作 次运算. -
- )2=
)2= ,求代数式
,求代数式 的值为 .
的值为 . (2)
(2) 
 (2)
(2)
 +1)2-(2
+1)2-(2 2-2
2-2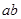 -4
-4 2,N=4
2,N=4 .
.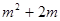 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号