[海南]2012届海南省高三高考极限压轴卷理科数学试卷
已知集合 ,
, ,则
,则 =
=
A.﹛ | | <-5,或 <-5,或 >-3﹜ >-3﹜ |
B.﹛ |-5< |-5< <5﹜ <5﹜ |
C.﹛ |-3< |-3< <5﹜ <5﹜ |
D.﹛ | | <-3,或 <-3,或 >5﹜ >5﹜ |
下列命题中正确命题的个数是
(1) 是
是 的充分必要条件;
的充分必要条件;
(2)若 且
且 ,则
,则 ;
;
(3)若将一组样本数据中的每个数据都加上同一个常数后,则样本的方差不变;
(4)设随机变量 服从正态分布N(0,1),若
服从正态分布N(0,1),若 ,则
,则
| A.4 | B.3 | C.2 | D.1 |
在同一平面直角坐标系中,函数 的图象与
的图象与 的图象关于直线
的图象关于直线 对称.而函数
对称.而函数 的图象与
的图象与 的图象关于
的图象关于 轴对称,若
轴对称,若 ,则
,则 的值是
的值是
A. |
B. |
C. |
D. |
过双曲线 的左焦点
的左焦点 ,作圆
,作圆 的
的
切线,切点为 ,延长
,延长 交双曲线右支于点
交双曲线右支于点 ,若
,若 ,则双曲线的离心率为
,则双曲线的离心率为
A. |
B. |
C. |
D. |
在 中,
中, 是
是 边中点,角
边中点,角 ,
, ,
, 的对边分别是
的对边分别是 ,
, ,
, ,
,
若

 ,则
,则 的形状为
的形状为
| A.直角三角形 | B.钝角三角形 |
| C.等边三角形 | D.等腰三角形但不是等边三角形. |
已知抛物线 ,过其焦点且斜率为1的直线交抛物线于
,过其焦点且斜率为1的直线交抛物线于 、
、 两点,若线段
两点,若线段 的中点的纵坐标为2,则该抛物线的准线方程为 .
的中点的纵坐标为2,则该抛物线的准线方程为 .
四棱锥 的三视图如右图所示,四棱锥
的三视图如右图所示,四棱锥 的五个顶点都在一个球面上,
的五个顶点都在一个球面上, 、
、 分别是棱
分别是棱 、
、 的中点,直线
的中点,直线 被球面所截得的线段长为
被球面所截得的线段长为 ,则该球表面积为 .
,则该球表面积为 .
(本小题满分12分)
已知公差不为零的等差数列 的前4项和为10,且
的前4项和为10,且 成等比数列.
成等比数列.
(Ⅰ)求通项公式 ;
;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分12分)
某班甲、乙两名同学参加l00米达标训练,在相同条件下两人l0次训练的成绩(单位:秒)如下:
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 甲 |
11.6 |
12.2 |
13.2 |
13.9 |
14.0 |
11.5 |
13.1 |
14.5 |
11.7 |
14.3 |
| 乙 |
12.3 |
13.3 |
14.3 |
11.7 |
12.0 |
12.8 |
13.2 |
13.8 |
14.1 |
12.5 |
(I)请作出样本数据的茎叶图;如果从甲、乙两名同学中选一名参加学校的100米比赛,从成绩的稳定性方面考虑,选派谁参加比赛更好,并说明理由(不用计算,可通过统计图直接回答结论).
(Ⅱ)从甲、乙两人的10次训练成绩中各随机抽取一次,求抽取的成绩中至少有一个比12.8秒差的概率.
(Ⅲ)经过对甲、乙两位同学的多次成绩的统计,甲、乙的成绩都均匀分布在[11.5,14.5]
之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于0.8秒的概率.
(本小题满分12分)
如图,正方形 与梯形
与梯形 所在的平面互相垂直,
所在的平面互相垂直, ,
, ∥
∥ ,
,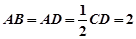 ,点
,点 在线段
在线段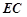 上.
上.
(I)当点 为
为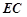 中点时,求证:
中点时,求证: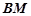 ∥平面
∥平面 ;
;
(II)当平面 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为 时,求三棱锥
时,求三棱锥 的体积.
的体积.
(本小题满分12分)
如图所示,点 在圆
在圆 :
: 上,
上,
 轴,点
轴,点 在射线
在射线 上,且满足
上,且满足
 .
.
(Ⅰ)当点 在圆
在圆 上运动时,求点
上运动时,求点 的轨迹
的轨迹 的方程,并根据
的方程,并根据 取值说明轨迹
取值说明轨迹 的形状.
的形状.
(Ⅱ)设轨迹 与
与 轴正半轴交于点
轴正半轴交于点 ,与
,与 轴正半轴交于点
轴正半轴交于点 ,直线
,直线 与轨迹
与轨迹 交于点
交于点 、
、 ,点
,点 在直线
在直线 上,满足
上,满足 ,求实数
,求实数 的值.
的值.
(本小题满分12分)
已知函数 ,曲线
,曲线 在点(
在点( )处的
)处的
切线方程是
(Ⅰ)求 的值;
的值;
(Ⅱ)设 若当
若当 时,恒有
时,恒有 ,求
,求 的取值范围.
的取值范围.
(本小题满分10分)选修4—1:几何证明选讲
如图, 是△
是△ 的外接圆,D是的中点,BD交AC于E.
的外接圆,D是的中点,BD交AC于E.
(Ⅰ)求证: ;
;
(Ⅱ)若 ,O到AC的距离为1,求⊙O的半径
,O到AC的距离为1,求⊙O的半径 .
.
(本小题满分10分)选修4—4:坐标系与参数方程
平面直角坐标系中,直线 的参数方程是
的参数方程是 (
( 为参数),
为参数),
以坐标原点为极点, 轴的正半轴为极轴,建立极坐标系,已知曲线
轴的正半轴为极轴,建立极坐标系,已知曲线 的极坐标方程为
的极坐标方程为
 .
.
(Ⅰ)求直线 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线 与曲线
与曲线 相交于
相交于 、
、 两点,求
两点,求 .
.
 满足
满足 (
( 是虚数单位),则
是虚数单位),则 =
=


 ,其中
,其中 ,对应法则
,对应法则 ,若对实数
,若对实数 ,在集合A中不存在元素
,在集合A中不存在元素 使得
使得 ,则k的取值范围是
,则k的取值范围是



 满足
满足 ,其图象与直线
,其图象与直线 的某两个交点横坐标为
的某两个交点横坐标为 ,
, 的最小值为
的最小值为 ,则
,则  ,
,
 ,
,
 ,
, 满足条件
满足条件 ,则
,则 的最小值为
的最小值为
 的展开式中含有
的展开式中含有 的正整数幂的项的个数是
的正整数幂的项的个数是 和曲线
和曲线 围成的图形面积是( )
围成的图形面积是( )



 (
( )与函数
)与函数 ,
, 的图象分别交于
的图象分别交于 、
、 两点,当
两点,当 最小时,
最小时, 值是
值是



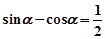 ,
,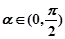 ,则
,则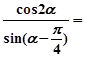 .
. 函数值的程序,若输出的
函数值的程序,若输出的 值为4,则输入的
值为4,则输入的 值是 .
值是 .
 .
. ;
; .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号