[浙江]2011－2012学年浙江杭州萧山瓜沥片七年级5月四科联赛数学试卷

下列方程中，其中二元一次方程的个数是（    ）
①4x+5=1；②3x—2y=1；③；④xy+y=14

下列图中的“笑脸”，由图（1）按逆时针方向旋转90º得到的是（   ）

（1）       A           B         C          D

下列计算中，结果错误的是（    ）

下图中，正确画出△ABC的 AC边上的高的是 （   ）

A             B              C              D

下列从左到右的变形，是因式分解的是（   ）

如图：PD⊥AB，PE⊥AC，垂足分别为D、E，且AP平分∠BAC，则△APD≌△APE的理由是（　　）

A.SAS　  B.HL　  C.SSS  　D.AAS

有五条线段长分别为1，3，5，7，9，从中任取三条，能组成三角形的概率是（   ）

若，则的值为（    ）

如图，O是边长为的正方形ABCD的中心，将一块半径足够长，圆心为直角的扇形纸板的圆心放在O点处，并将纸板的圆心绕O旋转，求正方形ABCD的边被纸板覆盖部分的面积为（   ）

A．

B．

C．

D．

初一某班有学生60名，其中参加数学兴趣小组的有36人，参加英语小组的人数比参加数学小组的人数少5人，并且这两个小组都不参加的人数比两个小组都参加的人数的少1人，则同时参加这两个小组的人数是（   ）

某种细菌的存活时间只有0.000 012秒，若用科学记数法表示此数据应为________秒

多项式4x²＋3mx＋9是另一个多项式的平方，则m=     

若x,y是正整数，且，则x+y=_________

用黑白两种颜色的正六边形地面砖按如图所示的规律，拼成若干图案，请推算

（1）第10个图案中白色的地面砖需____   _块；
（2）第n个图案中需黑白地面砖共____   块．

如图，由6个正方形构成一个大长方形，已知其中最小的正方形面积是1cm²,则大长方形的面积为________ cm²

如图，△ABC中∠A=30°，E是AC边上的点，先将△ABE沿着BE翻折，翻折后△ABE的AB边交AC于点D，又将△BCD沿着BD翻折，C点恰好落在BE上，此时∠CDB＝82°，则原三角形的∠B ＝_______度．

计算

判断下列事件哪些是必然事件，哪些是不确定事件，哪些是不可能事件？
事件1：三条边对应相等的两个三角形全等
事件2：三个角对应相等的两个三角形全等
事件3：有两边和其中一边上的中线对应相等的两个三角形全等
事件4：有两边和其中一边的对角对应相等的两个三角形全等
事件5：有两角和其中一角的对边对应相等的两个三角形全等
对于事件4，现在我们通过画图来说明。例如，已知∠α和线段a，b.用直尺和圆规作△ABC，使得∠C=∠α，AC=b,AB=a

对于任意的有理数a，b，c，d，我们规定如： ，根据这一规定，解答下列问题
化简
若x，y同时满足=5，，求x+y的值

如图，CD⊥AB于点D，BE⊥AC于点E，BE，CD相交于点O，且AO平分∠BAC,则BE与CD相等，请说明理由.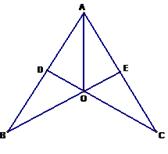

小明、小亮和小强三人准备下象棋，他们约定用“抛硬币”的游戏方式来确定哪两人先下棋，规则：三人手中各持有一枚质地均匀的硬币，他们同时将手中硬币抛落到水平地面为一个回合，落地后，三枚硬币中，恰有两枚正面向上或者反面向上的两人先下棋；若三枚硬币均正面向上或反面向上则不能确定哪两人先下棋。
请你完成下面表示游戏一个回合所有可能出现的结果的树状图（你也可自己另外画树状图或列表格）；
求一个回合能确定两人先下棋的概率．

2011年10月29日萧山“花木之乡”新街镇举行全民运动会，新街中学组织180名七年级学生和224名八年级学生参加开幕式的演出，其中表演队伍中八年级女生比七年级女生多24人，八年级男生是七年级男生的1.2倍。为了接送这些学生与31位带队老师，学校租用了45座和60座的大客车一共9辆，并且刚好能坐满。45座大客车的租金是500元/辆，60座大客车的租金是600元/辆。
求整个表演队伍中有女生，男生各多少人？
租用了45座大客车 ▲ 辆，60座大客车 ▲ 辆，租车费用是 ▲ 元。（直接写出答案）
你能否找出更合算的租车方案来吗？如果没有，请说明理由；如果有，请你写出租车方案和租车费用。

图a是一个长为2 m、宽为2 n的长方形，现在沿图中虚线剪开，平均分成四块全等的小长方形，然后按图b的形状拼成一个正方形。
你认为图b中的阴影部分的正方形的边长等于多少?

图a                    图b
观察图b你能写出下列三个代数式之间的等量关系吗?
代数式:                  
根据（2）题中的等量关系，解决如下问题：
若，求的值。
如右图，现有正方形甲2张，正方形乙2张，长方形丙5张，请你将它们组合拼成一个大长方形（画出图示），并运用面积之间的关系，将多项式2a²+5ab+2b²分解因式．