[江苏]2012届江苏省无锡市惠山区九年级5月模拟考试数学试卷
下列运算中,结果正确的是
A.a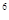 ÷a ÷a =a =a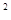 |
B.(2ab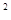 ) )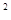 =2a =2a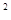 b b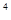 |
C.a·a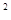 =a =a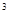 |
D.(a+b)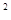 =a =a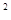 +b +b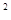 |
下列命题是假命题的是
| A.三角形的内角和是180 ° | B.多边形的外角和都等于360° |
| C.五边形的内角和是900° | D.三角形的一个外角等于和它不相邻的两个内角的和 |
已知⊙O1和⊙O2的半径分别为2cm和3cm,两圆的圆心距为5cm,则两圆的位置关
系是
| A.外切 | B.外离 | C.相交 | D.内切 |
在共有15人参加的“我爱祖国”演讲比赛中,参赛选手要想知道自己是否能进入前8名,除了知道自己的成绩以外,还需要知道全部成绩的
| A.平均数 | B.众数 | C.方差 | D.中位数 |
如图是一个圆锥形冰淇淋,已知它的母线长是13cm,高是12cm,则这个圆锥形冰淇淋的底面面积是
A. cm2 cm2 |
B. cm2 cm2 |
C. cm2 cm2 |
D. cm2 cm2 |

如图,已知双曲线 经过Rt△OAB斜边OA的中点D,且与直角边AB相交于点C.则△AOC的面积为
经过Rt△OAB斜边OA的中点D,且与直角边AB相交于点C.则△AOC的面积为
A.9 B.6 C. 4.5 D.3
如图,四边形ABCD中,DC∥AB,BC=1,AB=AC=AD=2,则BD的长为
| A. | B. | C.3 | D.2 |

国家游泳中心“水立方”是北京2008年奥运会场馆之一,它的外层膜的展开面积约为260 000平方米,用科学记数法表示是 平方米.
“爱心小组”的九位同学为灾区捐款,捐款金额分别为10,10,11,15,17,17,18,20,20(单位:元).那么这组数据的中位数是
如图,已知AB是⊙O的弦,半径OA=1cm,∠AOB=120 ,⊙O上一动点P从A点出发,沿逆时针方向运动一周,当S
,⊙O上一动点P从A点出发,沿逆时针方向运动一周,当S =S
=S 时,则点P所经过的弧长是
时,则点P所经过的弧长是
图中所示是一条宽为1.5m的直角走廊,现有一辆转动灵活的手推车,其矩形平板面ABCD的宽AB为1m,若要想顺利推过(不可竖起来或侧翻)直角走廊,平板车的长AD不能超过_____m.
工商银行为改进在上下班高峰的服务水平,随机抽样调查了部分该行顾客在上下班高峰时从开始排队到办理业务所用的时间t(单位:分).
下面是这次调查统计分析得到的频数分布表和频数分布直方图.
| 分组 |
频数 |
频率 |
|
| 一组 |
0<t≤5 |
10 |
0.1 |
| 二组 |
5<t≤10 |
|
0.3 |
| 三组 |
10<t≤15 |
25 |
0.25 |
| 四组 |
15<t≤20 |
20 |
|
| 五组 |
20<t≤25 |
15 |
0.15 |
| 合计 |
|
1.00 |

在上表中填写所缺数据
补全频数分布直方图
据调查顾客对服务质量的满意程度与所用时间t的关系如下:
| 所用时间t |
顾客满意程度 |
| 0<t≤10 |
比较满意 |
| 10<t≤15 |
基本满意 |
| t>15 |
比较差 |
请结合频数分布表和频数分布直方图回答:本次调查中,处于中位数的顾客对服务质量的满意程度为 ,顾客从开始排队到办理业务所用的时间平均为
分钟,用以上调查结果来判断工商银行全天的服务水平合理吗?为什么?
6张不透明的卡片,除正面画有不同的图形外,其它均相同,把这6张卡片洗匀后,正面向下放在桌上,另外还有与卡片上图形形状完全相同的地板砖若干块,所有地板砖的长都相等。从这6张卡片中随机抽取一张,与卡片上图形形状相对应的这种地板砖能进行平面镶嵌的概率是多少?
从这6张卡片中随机抽取2张,利用列表或画树状图计算:与卡片上图形形状相对应的这两种地板砖能进行平面镶嵌的概率是多少?

如图,某人在一栋高层建筑顶部C处测得山坡坡脚A处的俯角为60°,又测得山坡上一棵小树树干与坡面交界P处的俯角为45°,已知OA=50米,山坡坡度为 (即tan∠PAB=
(即tan∠PAB= ,其中PB⊥AB ),且O、A、B在同一条直线上.
,其中PB⊥AB ),且O、A、B在同一条直线上. 求此高层建筑的高度OC.(结果保留根号形式.);
求坡脚A处到小树树干与坡面交界P处的坡面距离AP的长度. (人的高度及测量仪器高度忽略不计,结果保留3个有效数字.)

小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发x min后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).A点所表示的实际意义是 ;= ;
求出AB所在直线的函数关系式;
如果小刚上坡平均速度是小亮上坡平均速度的一半,那么两人出发后多长时间第一次相遇?

如图1是两个有一边重合的正三角形,那么由其中一个正三角形绕平面内某一点旋转后能与另一个正三角形重合,平面内可以作为旋转中心的点有_ 个.
如图2是两个有一边重合的正方形,那么由其中一个正方形绕平面内某一点旋转后能与另一个正方形重合,平面内可以作为旋转中心的点有_ 个.
如图3是两个有一边重合的正五边形,那么由其中一个正五边形绕平面内某一点旋转后能与另一个正五边形重合,平面内可以作为旋转中心的点有_ 个.
如图4是两个有一边重合的正六边形,那么由其中一个正六边形绕平面内某一点旋转后能与另一个正六边形重合,平面内可以作为旋转中心的点有_ 个.
拓展探究:两个有一边重合的正n(n≥3)边形,那么由其中一个正n边形绕平面内某一点旋转后能与另一个正n边形重合,平面内可以作为旋转中心的点有多少个?(直接写结论)
|
|


|
|


已知直线 与
与 轴
轴 轴分别交于点A和点B,点B的坐标为(0,6)
轴分别交于点A和点B,点B的坐标为(0,6)求的
 值和点A的坐标;
值和点A的坐标;在矩形OACB中,某动点P从点B出发以每秒1个单位的速度沿折线B-C-A运动.运动至点A停止.直线PD⊥AB于点D,与
 轴交于点E.设在矩形OACB中直线PD未扫过的面积为S,运动时间为 t.
轴交于点E.设在矩形OACB中直线PD未扫过的面积为S,运动时间为 t.
①求 与t的函数关系式;
与t的函数关系式;
②⊙Q是△OAB的内切圆,问:t为何值时,PE与⊙Q相交的弦长为2.4 ?
 中自变量x的取值范围是
中自变量x的取值范围是 



 的自变量
的自变量 的取值范围是
的取值范围是 =
= 的中位线
的中位线 上任意一点,若梯形
上任意一点,若梯形

 .
.
 并写出其所有自然数解
并写出其所有自然数解

 粤公网安备 44130202000953号
粤公网安备 44130202000953号