[山东]2012届山东省高考模拟预测卷理科数学试卷(二)
 是 ( )
是 ( )
A.最小正周期为 的偶函数 的偶函数 |
B.最小正周期为 的奇函数 的奇函数 |
C.最小正周期为 的偶函数 的偶函数 |
D.最小正周期为 的奇函数 的奇函数 |
下列结论错误的是( )
A.命题“若 ,则 ,则 ”与命题“若 ”与命题“若 则 则 ”互为逆否命题; ”互为逆否命题; |
B.命题 ,命题 ,命题 则 则 为真; 为真; |
C.“若 则 则 ”的逆命题为真命题; ”的逆命题为真命题; |
D.若 为假命题,则 为假命题,则 、 、 均为假命题. 均为假命题. |
如右图所示是某一容器的三视图,现向容器中匀速注水,容器中水面的高度 随时间
随时间 变化的可能图象是( )
变化的可能图象是( )

A. B. C. D.
设 为三条不同的直线,
为三条不同的直线, 为一个平面,下列命题中正确的个数是( )
为一个平面,下列命题中正确的个数是( )
①若 ,则
,则 与
与 相交
相交
②若 则
则
③若 ||
|| ,
, ||
|| ,
, ,则
,则
④若 ||
|| ,
, ,
, ,则
,则 ||
||
| A.1 | B.2 | C.3 | D.4 |
把函数 的图象向左平移
的图象向左平移 个单位,再将图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)所得的图象解析式为
个单位,再将图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)所得的图象解析式为 ,则( )
,则( )
A. |
B. |
C. |
D. |
已知正六棱柱的12个顶点都在一个半径为3的球面上,当正六棱柱的体积最大(柱体体积=底面积 高)时,其高的值为( )
高)时,其高的值为( )
A. |
B. |
C. |
D. |
如图,在正三角形 中,
中, 分别为各边的中点,
分别为各边的中点, 分别为
分别为 的中点,将
的中点,将 沿
沿 折成正四面体
折成正四面体 ,则四面体中异面直线
,则四面体中异面直线 与
与 所成的角的余弦值为 .
所成的角的余弦值为 . 
△ABC中,a,b,c分别是角A,B,C的对边,向量 =(2sinB,2-cos2B),
=(2sinB,2-cos2B), ,
, ⊥
⊥ .
.
(Ⅰ)求角B的大小;
(Ⅱ)若 ,b=1,求c的值.
,b=1,求c的值.
某厂家拟资助三位大学生自主创业,现聘请两位专家,独立地对每位大学生的创业方案进行评审.假设评审结果为“支持”或“不支持”的概率都是 .若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助,令
.若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助,令 表示该公司的资助总额.
表示该公司的资助总额.
(Ⅰ)写出 的分布列;
的分布列;
(Ⅱ)求数学期望 .
.
在各项均为负数的数列 中,已知点
中,已知点 在函数
在函数 的图像上,且
的图像上,且 .
.
(Ⅰ)求证:数列 是等比数列,并求出其通项;
是等比数列,并求出其通项;
(Ⅱ)若数列 的前
的前 项和为
项和为 ,且
,且 ,求
,求 .
.
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF, BCF=
BCF= CEF=
CEF= ,AD=
,AD= ,EF=2.
,EF=2.
(Ⅰ)求证:AE//平面DCF;
(Ⅱ)当AB的长为何值时,二面角A-EF-C的大小为 .
.
已知椭圆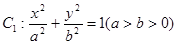 的离心率为
的离心率为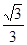 ,直线l:y=x+2与以原点为圆心、椭圆C1的短半轴长为半径的圆O相切。
,直线l:y=x+2与以原点为圆心、椭圆C1的短半轴长为半径的圆O相切。
(Ⅰ)求椭圆C1的方程;
(Ⅱ)设椭圆C1的左焦点为F1,右焦点为F2,直线l1过点F1,且垂直于椭圆的长轴,动直线l2垂直于l1,垂足为点P,线段PF2的垂直平分线交l2于点M,求点M的轨迹C2的方程;
(Ⅲ)设C2与x轴交于点Q,不同的两点R、S在C2上,且 满足 ,求
,求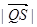 的取值范围。
的取值范围。
 ,
, ,若
,若 ,则a的取值范围是( )
,则a的取值范围是( )



 与
与 所围成图形的面积,其中正确的是( )
所围成图形的面积,其中正确的是( )



 首项与公比分别是复数
首项与公比分别是复数 是虚数单位
是虚数单位 的实部与虚部,则数列
的实部与虚部,则数列 项的和为( )
项的和为( )



 ,则A、B、C三点共线的充要条件为( )
,则A、B、C三点共线的充要条件为( ) B.
B. C.
C. D.
D.
 是
是 的零点,若
的零点,若 ,则
,则 的值满足( )
的值满足( )



 ,当0
,当0 时,
时, 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( )


 和
和 的夹角为
的夹角为 ,
, ,则
,则
 的最小值为
的最小值为  中,若
中,若 ,则
,则 外接圆半径
外接圆半径 .运用类比方法,若三棱锥的三条侧棱两两互相垂直且长度分别为
.运用类比方法,若三棱锥的三条侧棱两两互相垂直且长度分别为 ,则其外接球的半径
,则其外接球的半径 =
= 
 时,求
时,求 的最大值;
的最大值; ,(
,( ),其图象上任意一点
),其图象上任意一点 处切线的斜率
处切线的斜率 ≤
≤ 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,
, ,方程
,方程 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号