[江西]2012届江西省南昌市九年级下学期4月考数学卷
某市计划从2008年到2012年新增林地面积253万亩,253万亩用科学记数法表示正确的是( )
A. 亩 亩 |
B. 亩 亩 |
C. 亩 亩 |
D. 亩 亩 |
如图,在△ABC中,D是BC延长线上一点,∠B = 40°,∠ACD = 120°,则∠A等于( )
| A.90° | B.80° | C.70° | D.60° |
如图,在下列条件中,不能证明△ABD≌△ACD的是条件( ).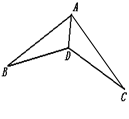
| A.∠B=∠C,BD=DC | B.∠ADB=∠ADC,BD=DC |
| C.∠B=∠C,∠BAD=∠CAD | D.BD=DC, AB=AC |
如图,是某复印店复印收费y(元)与复印面数(8开纸)x(面)的函数图象,那么从图象中可看出,复印超过100面的部分,每面收费( )
| A.0.4元 | B.0.45 元 | C.约0.47元 | D.0.5元 |
等腰三角形ABC在直角坐标系中,底边的两端点坐标分别是(-3,m),(5,m),则能确定的是它的( )
| A.一腰的长 | B.底边的长 | C.周长 | D.面积 |
生产季节性产品的企业,当它的产品无利润时就会及时停产.现有一生产季节性产品的企业,其一年中获得的利润 和月份
和月份 之间函数关系式为
之间函数关系式为 ,则该企业一年中应停产的月份是( )
,则该企业一年中应停产的月份是( )
| A.1月、2月、3月 | B.2月、3月、12月 |
| C.1月、2月、12月 | D.1月、11月、12月 |
.如图,A,B的坐标为(2,0),(0,1)若将线段 平移至
平移至 ,则
,则 的值为( )
的值为( )
| A.2 | B.3 | C.4 | D.5 |

将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图1.在图2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换.若骰子的初始位置为图1所示的状态,那么按上述规则连续完成10次变换后,骰子朝上一面的点数是( )
| A.6 | B.5 | C.3 | D.2 |
如图,有一圆形展厅,在其圆形边缘上的点 处安装了一台监视器,它的监控角度是
处安装了一台监视器,它的监控角度是 .为了监控整个展厅,最少需在圆形边缘上共安装这样的监视器 台.
.为了监控整个展厅,最少需在圆形边缘上共安装这样的监视器 台.
小华有3张卡片,小明有2张卡片,卡片上的数字如图所示.小华和小明分别从自己的卡片中随机抽取一张.请用画树状图(或列表)的方法,求抽取的两张卡片上的数字和为6的概率.
如图1,正方形ABCD是一个6 × 6网格电子屏的示意图,其中每个小正方形的边长为1.位于AD中点处的光点P按图2的程序移动.求光点P经过的路径总长(结果保留π).
如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;
(1)先作△ABC关于直线 成轴对称的图形,再向上平移1个单位,得到△A1B1C1;
成轴对称的图形,再向上平移1个单位,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
某幼儿园在六一儿童节购买了一批牛奶.如果给每个小朋友分5盒;则剩下38盒,如果给每个小朋友分6盒,则最后小朋友不足5盒,但至少分得1盒.问:该幼儿园至少有多少名小朋友?最多有多少名小朋友.
某商场家电销售部有营业员20名,为了调动营业员的积极性,决定实行目标管理,即确定一个月的销售额目标,根据目标完成情况对营业员进行适当的奖惩.为此,商场统计了这20名营业员在某月的销售额,数据如下:(单位:万元)
25 26 21 17 28 26 20 25 26 30
20 21 20 26 30 25 21 19 28 26
(1)请根据以上信息完成下表:
| 销售额(万元) |
17 |
19 |
20 |
21 |
25 |
26 |
28 |
30 |
| 频数(人数) |
1 |
1 |
3 |
3 |
|
|
2 |
2 |
(2)上述数据中,众数是 万元,中位数是 万元,平均数是 万元;
(3)如果将众数作为月销售额目标,能否让至少一半的营业员都能达到目标?请说明理由.
南昌市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?
已知双曲线 和直线AB的图象交于点A(-3,4),AC⊥x轴于点C.
和直线AB的图象交于点A(-3,4),AC⊥x轴于点C.
(1)求双曲线 的解析式;
的解析式;
(2)当直线AB绕着点A转动时,与x轴的交点为B(a,0),并与双曲线 另一支还有一个交点的情形下,求△ABC的面积S与a之间的函数关系式.,并指出a的取值范围.
另一支还有一个交点的情形下,求△ABC的面积S与a之间的函数关系式.,并指出a的取值范围.
一量角器所在圆的直径为10厘米,其外缘有A、B两点,其读数、分别为71°和47°.
(1).劣弧AB所对圆心角是多少度?
(2).求劣弧AB的长;
(3)问A、B之间的距离是多少?(可用计算器,精确到0.1)
如图,BD是⊙O的直径,A、C是⊙O上的两点,且AB=AC,AD与BC的延长线交于点E.
(1)求证:△ABD∽△AEB;
(2)若AD=1,DE=3,求⊙O半径的长.
(1)观察发现如题(a)图,若点A,B在直线 同侧,在直线
同侧,在直线 上找一点P,使AP+BP的值最小. 做法如下:作点B关于直线
上找一点P,使AP+BP的值最小. 做法如下:作点B关于直线 的对称点
的对称点 ,连接
,连接 ,与直线
,与直线 的交点就是所求的点P 再如题(b)图,在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小. 做法如下:作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为 .
的交点就是所求的点P 再如题(b)图,在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小. 做法如下:作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为 . 
(2)实践运用
如题(c)图,已知⊙O的直径CD为4,弧AD所对圆心角的度数为60°,点B是弧AD的中点,请你在直径CD上找一点P,使BP+AP的值最小,并求BP+AP的最小值.
(3)拓展延伸
如题(d)图,在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD.保留
作图痕迹,不必写出作法.
如图:在平面直角坐标系中,将长方形纸片ABCD的顶点B与原点O重合,BC边放在x轴的正半轴上,AB=3,AD=6,将纸片沿过点M的直线折叠(点M在边AB上),使点B落在边AD上的E处(若折痕MN与x轴相交时,其交点即为N),过点E作EQ⊥BC于Q,交折痕于点P。
(1)①当点 分别与AB的中点、A点重合时,那么对应的点P分别是点
分别与AB的中点、A点重合时,那么对应的点P分别是点 、
、 ,则
,则 ( , )、
( , )、 ( , );②当∠OMN=60°时,对应的点P是点
( , );②当∠OMN=60°时,对应的点P是点 ,求
,求 的坐标;
的坐标;
(2)若抛物线 ,是经过(1)中的点
,是经过(1)中的点 、
、 、
、 ,试求a、b、c的值;
,试求a、b、c的值;
(3)在一般情况下,设P点坐标是(x,y),那么y与x之间函数关系式还会与(2)中函数关系相同吗(不考虑x的取值范围)?请你利用有关几何性质(即不再用 、
、 、
、 三点)求出y与x之间的关系来给予说明.
三点)求出y与x之间的关系来给予说明.
 2) 的结果是( )
2) 的结果是( )




 的酱油瓶,若不计绳子接头(
的酱油瓶,若不计绳子接头( 取3),则捆绳总长为 .
取3),则捆绳总长为 .
 ,求
,求  的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号