[河南]2012届河南省洛阳市示范高中高三下学期联考文科数学试卷
已知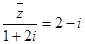 (
(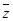 是
是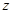 的共轭复数),则复数
的共轭复数),则复数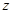 在复平面内对应的点位于( )
在复平面内对应的点位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
已知a,b是两条不重合的直线,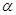 ,
, 是两个不重合的平面,下列命题中正确的是( )
是两个不重合的平面,下列命题中正确的是( )
A.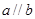 , ,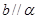 ,则 ,则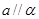 |
B.a,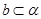 , ,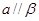 , ,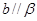 ,则 ,则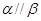 |
C.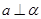 , ,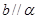 ,则 ,则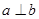 |
D.当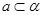 ,且 ,且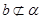 时,若 时,若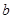 ∥ ∥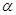 ,则 ,则 ∥ ∥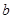 |
函数y=cos2x的图像可以看作由y= cos2x+sinxcosx的图像( )得到.
cos2x+sinxcosx的图像( )得到.
A.向左平移 个单位长度 个单位长度 |
B.向右平移 个单位长度 个单位长度 |
C.向左平移 单位长度 单位长度 |
D.向右平移 单位长度 单位长度 |
已知x是函数f(x)=2x+ 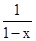 的一个零点.若
的一个零点.若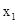 ∈(1,
∈(1, ),
),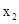 ∈(
∈( ,+
,+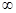 ),则
),则
A.f(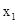 )<0,f( )<0,f(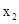 )<0 )<0 |
B.f(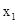 )<0,f( )<0,f(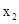 )>0 )>0 |
C.f(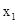 )>0,f( )>0,f(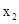 )<0 )<0 |
D.f(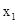 )>0,f( )>0,f(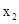 )>0 )>0 |
若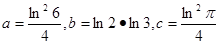 ,则a,b,c的大小关系是 ( )
,则a,b,c的大小关系是 ( )
| A.a>b>c | B.c>a>b | C.c>b>a | D.a>c>b |
已知双曲线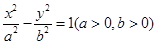 的左顶点与抛物线
的左顶点与抛物线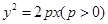 的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
A.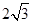 |
B.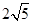 |
C.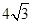 |
D.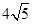 |
设函数f(x)=ex(sinx-cosx) (0≦x≦2012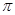 ),则函数f(x)的各极小值之和为( )
),则函数f(x)的各极小值之和为( )
A.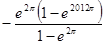 |
B.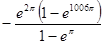 |
C.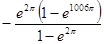 |
D.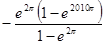 |
一个正三棱柱的侧棱长和底面边长相等,体积为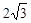 ,它的三视图中的俯视图如右图所示,左视图是一个矩形,则这个矩形的面积是_______.
,它的三视图中的俯视图如右图所示,左视图是一个矩形,则这个矩形的面积是_______.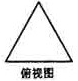
下图甲是某市有关部门根据对当地干部的月收入情况调查后画出的样本频率分布直方图,已知图甲中从左向右第一组的频数为4000.在样本中记月收入在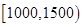 ,
,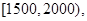
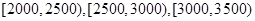 ,
,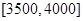 的人数依次为
的人数依次为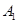 、
、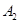 、……、
、……、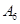 .图乙是统计图甲中月工资收入在一定范围内的人数的算法流程图,图乙输出的
.图乙是统计图甲中月工资收入在一定范围内的人数的算法流程图,图乙输出的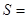 .(用数字作答)
.(用数字作答)
对于大于1的自然数m的三次幂可以用技术进行以下方式的“分裂”: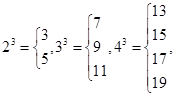 ……仿此,若
……仿此,若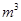 的“分裂数”中有一个是59,则m= .
的“分裂数”中有一个是59,则m= .
(本小题满分12分)
已知等差数列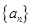 中,
中,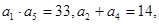
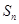 为数列
为数列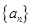 的前
的前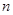 项和.
项和.
(1)求数列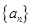 的通项公式;
的通项公式;
(2) 若数列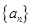 的公差为正数,数列
的公差为正数,数列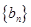 满足
满足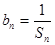 , 求数列
, 求数列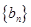 的前
的前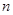 项和
项和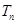
(本小题满分12分)有A、B、C、D、E五位工人参加技能竞赛培训.现分别从A、B二人在培训期间参加的若干次预赛成绩中随机抽取8次.用茎叶图表示这两组数据如下: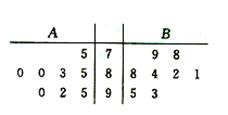
(Ⅰ) 现要从A、B中选派一人参加技能竞赛,从平均状况和方差的角度考虑,你认为派哪位工人参加合适?请说明理由;
(Ⅱ) 若从参加培训的5位工人中选2人参加技能竞赛,求A、B二人中至少有一人参加技能竞赛的概率.
如图,在四棱锥P—ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,PA=AB=4, G为PD中点,E点在AB上,平面PEC⊥平面PDC.

(Ⅰ)求证:AG⊥平面PCD;
(Ⅱ)求证:AG∥平面PEC;
(Ⅲ)求点G到平面PEC的距离.
(本小题满分12分)如图,在△ABC中,|AB|=|AC|=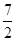 ,|BC|=2,以B、C为焦点的椭圆恰好过AC的中点P.
,|BC|=2,以B、C为焦点的椭圆恰好过AC的中点P.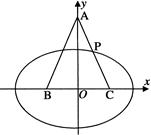
(Ⅰ)求椭圆的标准方程;
(Ⅱ) 过椭圆的右顶点作直线l与圆E:(x-1)2+y2=2相交于M、N两点,试探究点M、N能将圆E分割成弧长比值为1∶3的两段弧吗?若能,求出直线l的方程;若不能,请说明理由.
(本小题满分12分)已知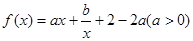 的图像在点
的图像在点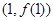 处的切线与直线
处的切线与直线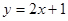 平行.
平行.
(1)求a,b满足的关系式;
(2)若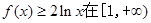 上恒成立,求a的取值范围;
上恒成立,求a的取值范围;
(本小题满分10分)选修4—1;几何证明选讲
如图,在△ABC 中,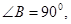 以AB为直径的⊙O交AC于D,点E为BC的中点,连接DE、AE, AE交⊙O于点F
以AB为直径的⊙O交AC于D,点E为BC的中点,连接DE、AE, AE交⊙O于点F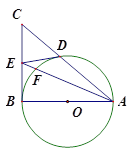
(Ⅰ) 求证: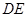 是⊙O的切线;
是⊙O的切线;
(Ⅱ) 若⊙O的直径为2,求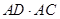 的值.
的值.
(本小题满分10分)选修4-4:坐标系与参数方程
在极坐标系中,已知圆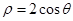 与直线
与直线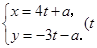 为参数)相切,求实数
为参数)相切,求实数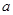 的值。
的值。
 ,
,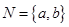 ,若
,若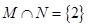 ,则
,则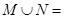 ( )
( )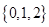 B、
B、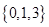 C、
C、 D、
D、
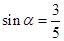 ,
,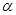 是第二象限的角,则
是第二象限的角,则 2
2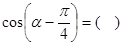
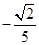
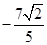

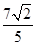
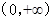 单调递增的函数是 ( )
单调递增的函数是 ( )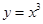
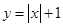
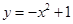
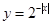
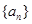 的公比为正数,且
的公比为正数,且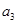 ·
·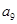 =2
=2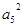 ,
, =1,则
=1,则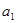 = ( )
= ( )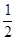

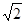
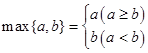 ,已知实数
,已知实数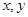 满足
满足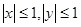 ,设
,设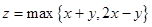 ,则
,则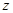 的取值范围是 ( )
的取值范围是 ( )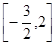
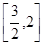
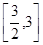
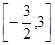
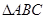 的外接圆半径为1,圆心为O,且
的外接圆半径为1,圆心为O,且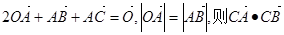 等于_________
等于_________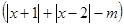 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号