[上海]2012届上海市闵行区高三上学期期末质量抽测理科数学试卷
如图,矩形OABC中,AB=1,OA=2,以B为圆心、BA为半径在矩形内部作弧,点P是弧上一动点, ,垂足为M,
,垂足为M, ,垂足为N,则四边形OMPN的周长的最小值为 .
,垂足为N,则四边形OMPN的周长的最小值为 .
已知线段AB上有10个确定的点(包括端点A与B). 现对这些点进行往返标数(从A→B→A→B→…进行标数,遇到同方向点不够数时就“调头”往回数)。如图:在点A上标1,称为点1,然后从点1开始数到第二个数,标上2,称为点2,再从点2开始数到第三个数,标上3,称为点3(标上数n的点称为点n),……,这样一直继续下去,直到1,2,3,…,2012都被标记到点上.则点2012上的所有标记的数中,最小的是 .
已知关于 的二元一次线性方程组的增广矩阵为
的二元一次线性方程组的增广矩阵为 ,记
,记 ,则此线性方程组有无穷多组解的充要条件是
,则此线性方程组有无穷多组解的充要条件是
[答]( )
A. . . |
B. 两两平行. 两两平行. |
C. . . |
D. 方向都相同. 方向都相同. |
设 、
、 是关于x的方程
是关于x的方程 的两个不相等的实数根,那么过两点
的两个不相等的实数根,那么过两点 ,
, 的直线与圆
的直线与圆 的位置关系是( )
的位置关系是( )
| A.相离. | B.相切. |
| C.相交. | D.随m的变化而变化 |
本题共有2个小题,第(1)小题满分5分,第(2)小题满分9分.
设双曲线 ,
, 是它实轴的两个端点,
是它实轴的两个端点, 是其虚轴的一个端点.已知其一条渐近线的一个方向向量是
是其虚轴的一个端点.已知其一条渐近线的一个方向向量是 ,
, 的面积是
的面积是 ,
, 为坐标原点,直线
为坐标原点,直线 与双曲线C相交于
与双曲线C相交于 、
、 两点,且
两点,且 .
.
(1)求双曲线 的方程;
的方程;
(2)求点 的轨迹方程,并指明是何种曲线.
的轨迹方程,并指明是何种曲线.
本题共有2个小题,第(1)小题满分6分,第(2)小题满分8分.
某地政府为改善居民的住房条件,集中建设一批经适楼房.用了1400万元购买了一块空地,规划建设8幢楼,要求每幢楼的面积和层数等都一致,已知该经适房每幢楼每层建筑面积均为250平方米,第一层建筑费用是每平方米3000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加80元.
(1)若该经适楼房每幢楼共 层,总开发费用为
层,总开发费用为 万元,求函数
万元,求函数 的表达式(总开发费用=总建筑费用+购地费用);
的表达式(总开发费用=总建筑费用+购地费用);
(2)要使该批经适房的每平方米的平均开发费用最低,每幢楼应建多少层?
本题共有3个小题,第(1)小题满分4分,第(2)小题满分5
分,第(3)小题满分7分.
将边长分别为1、2、3、…、n、n+1、…( )的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、……、第n个阴影部分图形.设前n个阴影部分图形的面积的平均值为
)的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、……、第n个阴影部分图形.设前n个阴影部分图形的面积的平均值为 .记数列
.记数列 满足
满足 ,
,

(1)求 的表达式;
的表达式;
(2)写出 的值,并求数列
的值,并求数列 的通项公式;
的通项公式;
(3)记 ,若不等式
,若不等式 有解,求
有解,求 的取值范围.
的取值范围.
 ,
, ,
, ,则
,则 .
. ,半径为1,则该扇形的圆心角的弧度数是 .
,半径为1,则该扇形的圆心角的弧度数是 . ,命题“若
,命题“若 ,则
,则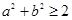 ”的否命题是 .
”的否命题是 . 为第二象限角,且
为第二象限角,且 ,则
,则 的值为 .
的值为 . 上一焦点与短轴两端点形成的三角形的面积为1,则
上一焦点与短轴两端点形成的三角形的面积为1,则 .
. 满足
满足 ,
, ,且
,且 与
与 的方向相反,则
的方向相反,则 与两点
与两点 ,若直线
,若直线 与线段
与线段 相交,则
相交,则 的取值范围是 .
的取值范围是 . ,则对于
,则对于 ,
,
 中,若
中,若 ,且
,且 ,则
,则 的大小为 .
的大小为 . ,则输出
,则输出 的值为 .
的值为 .
 的首项及公差均是正整数,前
的首项及公差均是正整数,前 项和为
项和为 ,且
,且 ,
, ,
, ,则
,则 = .
= .
 满足
满足 ,且当
,且当 时,
时, ,则函数
,则函数 的零点个数为 个.
的零点个数为 个. 的准线方程( )
的准线方程( ) .
. .
. .
. .
. 的图像与函数
的图像与函数 的图像关于
的图像关于 对称,则
对称,则
 .
. .
. .
. .
. ,规定向量的“*”运算为:
,规定向量的“*”运算为: .若
.若 .解不等式
.解不等式 .
. 在区间D上的最大值与最小值分别为
在区间D上的最大值与最小值分别为 与
与 .设函数
.设函数 ,
, .
. .
. 在
在 上单调递减,求
上单调递减,求 的取值范围;
的取值范围; .令
.令 .
. .试写出
.试写出 的表达式,并求
的表达式,并求 ;
; (其中I为
(其中I为 的定义域).若I恰好为
的定义域).若I恰好为 ,求b的取值范围,并求
,求b的取值范围,并求 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号