[广东]2011-2012学年广东省汕头市九年级第一学期期末数学试卷
下列各图是选自历届世博会徽中的图案,其中是中心对称图形的是( ).



A. B. C. D.
如图所示,在△ABC中,∠B=40°,将△ABC绕点A逆时针旋转至在△ADE处,使点B落在BC的延长线上的D点处,则∠BDE=( ).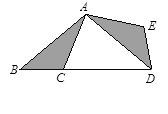
| A.90° | B.85° | C.80° | D.40° |
如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形的上底AD、下底BC以及腰AB均相切,切点分别是D、C、E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是( ).
A.9 B.10 C.12 D.14
如果关于x的一元二次方程x2+px+q=0的两根分别为x1=2,x2=1,那么q的值是____.
如图,P为等边△ABC的中心
画出将△ABP绕A逆时针旋转60°的图形;(不写画法,保留作图痕迹)
经过什么样的图形变换,可以把△ABP变换到右边的△CMN,请写出简要的文字说明
小红和小慧玩纸牌游戏.如图是同一副扑克中的4张牌的正面,将它们正面朝下洗匀后放在桌上,小红先从中抽出一张,小慧从剩余的3张牌中也抽出一张
请用树状图表示出两人抽牌可能出现的所有结果
求抽出的两张牌都是偶数的概率
如右图所示,已知圆锥底面半径r=10cm,母线长为40cm
求它的侧面展开图的圆心角和表面积
若一甲虫从A点出发沿着圆锥侧面行到母线SA的中点B,请你动脑筋想一想它所走的最短路线是多少?为什么?
观察下列方程及其解的特征:
(1) 的解为
的解为 ; (2)
; (2) 的解为
的解为 ;
;
(3) 的解为
的解为 ; …… ……
; …… ……
解答下列问题请猜想:方程
 的解为 ;
的解为 ;请猜想:关于
 的方程
的方程 的解为
的解为 ;(3)下面以解方程
;(3)下面以解方程 为例,验证(1)中猜想结论的正确性
为例,验证(1)中猜想结论的正确性
如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.
判断直线CD与⊙O的位置关系,并说明理由;
若⊙O的半径为1,求图中阴影部分的面积(结果保留π)




 = .
= .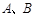 在数轴上对应的数分别为-2,
在数轴上对应的数分别为-2, ,且两点关于原点对称,则
,且两点关于原点对称,则 的值为____.
的值为____.
 (a>0)
(a>0)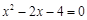
 的一元二次方程
的一元二次方程 ,其根的判别式的值为1,求m的值及该方程的根.
,其根的判别式的值为1,求m的值及该方程的根.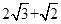 和
和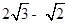 ,求该矩形的面积和对角线的长.
,求该矩形的面积和对角线的长. 的方程为
的方程为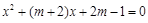
 是⊙
是⊙ 的直径,
的直径,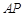 是⊙
是⊙ 是切点,
是切点, 与⊙
与⊙ .
.
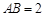 ,
,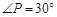 ,求
,求 为
为 是⊙
是⊙ 粤公网安备 44130202000953号
粤公网安备 44130202000953号