2012届高三一轮精品复习单元测试(12)数学试卷解析版
过坐标原点且与x2+y2 -4x+2y+ =0相切的直线的方程为 ( )
=0相切的直线的方程为 ( )
A.y=-3x或y= x x |
B.y=-3x或y=- x x |
C.y=-3x或y =- =- x x |
D.y=3x或y= x x |
函数f(x)=x3-3bx+3b在(0,1)内有极小值,则 ( )
| A.0<b<1 | B.b<1 | C.b>0 | D.b<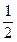 |
已知抛物线y2=2px(p>0)与一个定点M(p,p),则抛物线上与M点的距离最小的点为( )
| A.(0,0) | B.( ,p) ,p) |
C.( ) ) |
D.( ) ) |
已知函数 有绝对值相等,符号相反的极大值和极小值,则常数
有绝对值相等,符号相反的极大值和极小值,则常数 的值是( )
的值是( )
A. 或 或 |
B. 或 或 |
C. 或 或 |
D. 或 或 或 或 |
已知曲线y= x3+
x3+ ,则过点P(2
,则过点P(2 ,4)的切线方程是 ( )
,4)的切线方程是 ( )
| A.4x-y-4="0." | B.x-4y-4=0 . . |
| C.4x-4y-1="0." | D.4x+y-4=0. |
若曲线f(x)=x4-x在点P处的切线平行于直线3x-y=0,则点P的坐标为( )
| A.(1,3) | B.(-1,3) | C.(1,0) | D.(-1,0) |
函数f(x)=ax+loga(x+1)在[0,1]上的最大值与最小值之和为a,则a的值为 ( )
A. |
B. |
C.2 | D.4 |
已知函数f(x)=x3+ax2+bx+a2在x=1处有极值为10,则f(2)=( )
| A.13或18 | B.12或18 | C.11或18 | D.10或18 |
若函数f(x)=x3+x2+mx+1是R上的单调递增函数,则m的取值范围是______________
某厂生产某种产品 件的总成本
件的总成本 (万元),又知产品单价的平方与产品件数
(万元),又知产品单价的平方与产品件数 成反比,生产100件这样的产品的单价为50万元,则产量定为_____________时总利润最大?
成反比,生产100件这样的产品的单价为50万元,则产量定为_____________时总利润最大?
(本小题满分10分)一艘轮船在航行中的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问此轮船以何种速度航行时,能使行驶每公里的费用总和最小?
(本小题满分12分)已知函数f(x)= ,其中a , b , c是以d为公差的等差数列,且a>0,d>0.设
,其中a , b , c是以d为公差的等差数列,且a>0,d>0.设 [1-
[1- ]上,
]上, ,在
,在
 ,将点
,将点 A, B, C,
A, B, C,
(Ⅰ)求
(II)若⊿ABC有一边平行于x轴,且面积为 ,求a ,d的值.
,求a ,d的值.
(本小题满分12分)已知函数f(x)=x3+ax2+bx+c在x=- 与x=1时都取得极值.
与x=1时都取得极值.
(1)求a、b的值与函数f(x)的单调区间;
(2)xÎ〔-1,2〕,不等式f(x)<c2恒成立,求c的取值范围.
 在点
在点 处的切线与坐标轴围成的三角形面积为( )
处的切线与坐标轴围成的三角形面积为( )



 ,有
,有 ,且
,且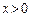 时,
时, ,则
,则 时 ( )
时 ( )



 的极值是 ( )
的极值是 ( ) 的极值是 ( )
的极值是 ( )



 ,函数
,函数 的最大值为1,最小值为
的最大值为1,最小值为 ,常数
,常数 的值是_____________.
的值是_____________.
 其中
其中
 的单调区间;
的单调区间; .
. ,讨论
,讨论 的单调性;
的单调性; 恒有
恒有 ,求
,求 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号