[安徽]2012 届安徽省皖南八校高三第一次联考文科数学试卷解析版
已知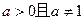 ,则“
,则“ ”是“
”是“ ”( )
”( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知双曲线 的右焦点为F,若过点F且倾斜角为30°
的右焦点为F,若过点F且倾斜角为30°
的直线与双曲线的一条渐近平行,则此双曲线离心率是 ( )
A. |
B.1 | C. |
D.2 |
某次跳水比赛中,七位评委为甲、乙两选手打出的分数的茎叶图如图 ,去掉一个最高分和一个最低分后,甲、乙两人的平均得分分别为
,去掉一个最高分和一个最低分后,甲、乙两人的平均得分分别为 ,则有( )
,则有( )
A. |
B. |
C. |
D. 有关 有关 |
已知关于x的方程 的两根为
的两根为 ,且满足
,且满足 ,
,
则点(m,n)所表示的平面区域面积为 ( )
A. |
B. |
C. |
D.2 |
①三角形纸片内有1个点,连同三角形的顶点共4个点,其中任意三点都不共线,
以这4个点为顶点作三角形,并把纸片剪成小三角形,可得小三角形个数为3个;②三角形
纸片内有2个点,连同三角形的顶点共5个点,其中任意三点都不共线,以这5个点为顶点
作三角形,并把纸片剪成小三角形,可得小三角形个数为5个,……
以此类推:三角形纸片内有15个点,连同三角形的顶点共18个点,若其中任意三点都不共线,以这些点为顶点作三角形,并把纸片剪成小三角形,则这样的小三角形个数为 个。(用数字作答)
(本小题满分12分)某汽车厂生产A、B两类轿车,每类轿车均有舒适型和标准型两种,某月的产量如下表:
按分层抽样的方法在该月生产的轿车中抽取50辆,其中A类轿车20辆。
(I)求x的值;
(II)用分层抽样的方法在B类轿车中抽取一个容量为6的样本,从样本中任意取2辆,求至少有一辆舒适轿车的概率。
(本小题满分12分)已知
(I)求 的最大值,及当取最大值时x的取值集合。
的最大值,及当取最大值时x的取值集合。
(II)在三角形ABC中a、b、c分别是角A、B、C所对的边,对定义域内任意 ,且b=1,c=2,求a的值。
,且b=1,c=2,求a的值。
(本小题满分12分)如图,在多面体ABDEC中,AE 平面ABC,BD//AE,且AC=AB=BC=AE=1,BD=2,F为CD中点。
平面ABC,BD//AE,且AC=AB=BC=AE=1,BD=2,F为CD中点。
(I)求证:EF//平面ABC;
(II)求证: 平面BCD;
平面BCD;
(III)求多面体ABDEC的体积。
(本小题满分13分)已知椭圆的中心在原点,焦点在y轴上,离心率为 ,且
,且
椭圆经过圆 的圆心C。
的圆心C。
(I)求椭圆的标准方程;
(II)设直线 与椭圆交于A、B两点,点
与椭圆交于A、B两点,点 且|PA|=|PB|,求直线
且|PA|=|PB|,求直线 的方程。
的方程。
(本小题满分13分)已知函数
(I)求函数 的单调区间;
的单调区间;
(II)若
 ,在(1,2)上为单调递
,在(1,2)上为单调递
减函数。求实数a的范围。
 的元素个数为( )
的元素个数为( ) 是虚数单位,
是虚数单位, 是纯虚数,则实数
是纯虚数,则实数 等于 ( )
等于 ( )
 的值为( )
的值为( )



 经过抛物线
经过抛物线 的焦点,则
的焦点,则 的
的



 的图像可能是 ( )
的图像可能是 ( )

 ,则向量a与b
,则向量a与b 图像在点
图像在点 的
的 图像在点M处的切线平行,则点M的坐标为 。
图像在点M处的切线平行,则点M的坐标为 。 ,已知
,已知
 ,
, 的序号为 。(填写所有正确结果的序号)
的序号为 。(填写所有正确结果的序号) ②
② ③
③ ④
④ ⑤
⑤
 的前n项和
的前n项和 与通项
与通项 之间满足关系
之间满足关系
 求
求
 ,求
,求 的前n项和
的前n项和
 粤公网安备 44130202000953号
粤公网安备 44130202000953号