2010年高考物理试题分类汇编——曲线运动、万有引力

如图，质量分别为m和M的两个星球$A$和$B$在引力作用下都绕O点做匀速周运动，星球$A$和$B$两者中心之间距离为L。已知$A$、$B$的中心和O三点始终共线，$A$$T=2\pi \sqrt{\frac{L^3}{G\left(M+m\right)}}$和$B$分别在O的两侧。引力常数为G。
⑴求两星球做圆周运动的周期。

⑵在地月系统中，若忽略其它星球的影响，可以将月球和地球看成上述星球$A$和$B$，月球绕其轨道中心运行为的周期记为$T_1$。但在近似处理问题时，常常认为月球是绕地心做圆周运动的，这样算得的运行周期$T_2$。已知地球和月球的质量分别为$5.98\times {10}^{24}kg$和$7.35\times {10}^{22}kg$ 。求$T_{{}^2}$与$T_1$两者平方之比。（结果保留3位小数）

一物体静置在平均密度为$\rho$的球形天体表面的赤道上。已知万有引力常量为$G$，若由于天体自转使物体对天体表面压力恰好为零，则天体自转周期为（）

已知地球同步卫星离地面的高度约为地球半径的6倍。若某行星的平均密度为地球平均密度的一半，它的同步卫星距其表面的高度是其半径的2.5倍，则该行星的自转周期约为（）

探测器绕月球做匀速圆周运动，变轨后在周期较小的轨道上仍做匀速圆周运动，则变轨后与变轨前相比（）

为了对火星及其周围的空间环境进行探测，我国预计于2011年10月发射第一颗火星探测器"萤火一号"。假设探测器在离火星表面高度分别为$h_1$和$h_2$的圆轨道上运动时，周期分别为$T_1$和$T_2$。火星可视为质量分布均匀的球体，且忽略火星的自转影响，万有引力常量为$G$。仅利用以上数据，可以计算出

如图，$ABD$为竖直平面内的光滑绝缘轨道，其中$AB$段是水平的，$BD$段为半径$R=0.2m$的半圆，两段轨道相切于$B$点，整个轨道处在竖直向下的匀强电场中，场强大小$E=5.0\times {10}^{3}V/m$。一不带电的绝缘小球甲，以速度${\upsilon }_0$沿水平轨道向右运动，与静止在$B$点带正电的小球乙发生弹性碰撞。已知甲、乙两球的质量均为$m=1.0\times {10}^{-2}kg$，乙所带电荷量$q=2.0\times {10}^{-5}C$，$g$取$10m/s^2$。(水平轨道足够长，甲、乙两球可视为质点，整个运动过程无电荷转移)
（1） 甲乙两球碰撞后，乙恰能通过轨道的最高点D，求乙在轨道上的首次落点到$B$点的距离；

（2）在满足(1)的条件下。求的甲的速度${\upsilon }_0$；

（3）若甲仍以速度${\upsilon }_0$向右运动，增大甲的质量，保持乙的质量不变，求乙在轨道上的首次落点到$B$点的距离范围。

月球与地球质量之比约为$1：80$，有研究者认为月球和地球可视为一个由两质点构成的双星系统，他们都围绕月球连线上某点$O$做匀速圆周运动。据此观点，可知月球与地球绕$O$点运动线速度大小之比约为（）

小明站在水平地面上，手握不可伸长的轻绳一端，绳的另一端系有质量为$m$的小球，甩动手腕，使球在竖直平面内做圆周运动，当球某次运动到最低点时，绳突然断掉。球飞离水平距离$d$后落地，如题24图所示，已知握绳的手离地面高度为$d$，手与球之间的绳长为$\frac{3}{4}d$，重力加速度为$g$，忽略手的运动半径和空气阻力。

（1）求绳断时球的速度大小$v_1$，和球落地时的速度大小$v_2$

（2）问绳能承受的最大拉力多大？
（3）改变绳长，使球重复上述运动。若绳仍在球运动到最低点时断掉，要使球抛出的水平距离最大，绳长应为多少？最大水平距离为多少？

1970年4月24日，我国自行设计、制造的第一颗人造地球卫星"东方红一号"发射成功，开创了我国航天事业的新纪元。"东方红一号"的运行轨道为椭圆轨道，其近地点的$M$和远地点的$N$的高度分别为439$km$和2384$km$，则（）

如图所示，一块橡皮用细线悬挂于$O$点，用铅笔靠着线的左侧水平向右匀速移动，运动中始终保持悬线竖直，则橡皮运动的速度（）

2009年5月，航天飞机在完成对哈勃空间望远镜的维修任务后，在$A$点从圆形轨道Ⅰ进入椭圆轨道Ⅱ，$B$为轨道Ⅱ上的一点，如图所示，关于航天飞机的运动，下列说法中正确的有（）

在游乐节目中，选手需借助悬挂在高处的绳飞越到水面的浮台上,小明和小阳观看后对此进行了讨论.如图所示，他们将选手简化为质量$m=60kg$的质点，选手抓住绳由静止开始摆动，此时绳与竖直方向夹角$\alpha ={53}^0$，绳的悬挂点O距水面的高度为$H=3m$.不考虑空气阻力和绳的质量，浮台露出水面的高度不计，水足够深。取重力加速度$g=10m/s^2$，$\sin \left({53}^0\right)=0.8$,$\cos \left({53}^0\right)=0.6$.

（1）求选手摆到最低点时对绳拉力的大小$F$；

（2）若绳长$l=2m$,选手摆到最高点时松手落入手中.设水对选手的平均浮力$f_1=800N$，平均阻力$f_2=700N$，求选手落入水中的深度$d$；

（3）若选手摆到最低点时松手，小明认为绳越长，在浮台上的落点距岸边越远；小阳却认为绳越短，落点距岸边越远，请通过推算说明你的观点。

太阳系中的8大行星的轨道均可以近似看成圆轨道。下列4幅图是用来描述这些行星运动所遵从的某一规律的图像。图中坐标系的横轴是$lg(T/T_0)$,纵轴是$lg(R/R_0)$;这里$T$和$R$分别是行星绕太阳运行的周期和相应的圆轨道半径，$T_0$和$R_0$分别是水星绕太阳运行的周期和相应的圆轨道半径。下列4幅图中正确的是（）

宇宙飞船以周期为$T$绕地地球作圆周运动时，由于地球遮挡阳光，会经历"日全食"过程，如图所示。已知地球的半径为$R$，地球质量为$M$，引力常量为$G$，地球处置周期为$T_0$，太阳光可看作平行光，宇航员在$A$点测出的张角为$\alpha$，则（）

在一次国际城市运动会中，要求运动员从高为$H$的平台上$A$点由静止出发，沿着动摩擦因数为$\mu$的滑道向下运动到$B$点后水平滑出，最后落在水池中。设滑道的水平距离为$L$，$B$点的高度$h$可由运动员自由调节（取$g=10m/s^2$）。求：
（1）运动员到达$B$点的速度与高度$h$的关系；
（2）运动员要达到最大水平运动距离，$B$点的高度$h$应调为多大？对应的最大水平距离$S_{max}$为多少？
（3）若图中$H=4m$，$L＝5m$，动摩擦因数$\mu =0.2$，则水平运动距离要达到$7m$，$h$值应为多少？

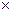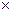$a$是地球赤道上一栋建筑，$b$是在赤道平面内作匀速圆周运动、距地面9.6${10}^{6}m$的卫星，$c$是地球同步卫星，某一时刻$b,c$刚好位于$a$的正上方（如图甲所示），经48$h$，$a,b,c$的大致位置是图中的（取地球半径$R$=6.4${10}^{6}m$，地球表面重力加速度$g=10m/s^2$，$\pi =\sqrt{10}$）（）

如图所示，空间有场强$E=0.5N/C$的竖直向下的匀强电场，长$l=0.3\sqrt{3}m$的不可伸长的轻绳一端固定于$O$点，另一端系一质量$m=0.01kg$的不带电小球$A$，拉起小球至绳水平后，无初速释放．另一电荷量$q=+0.1C$、质量与$A$相同的小球$P$，以速度$v_0=3\sqrt{3}m/s$水平抛出，经时间$t=0.2s$与小球$A$在$D$点迎面正碰并粘在一起成为小球$C$，碰后瞬间断开轻绳，同时对小球C施加一恒力，此后小球$C$与$D$点下方一足够大的平板相遇．不计空气阻力，小球均可视为质点，取$g=10m/s^2$．

（1）求碰撞前瞬间小球$P$的速度。

（2）若小球$C$经过路$s=0.09m$到达平板，此时速度恰好为$O$，求所加的恒力。

（3）若施加恒力后，保持平板垂直于纸面且与水平面的夹角不变，在$D$点下方任意改变平板位置，小球$C$均能与平板正碰，求出所有满足条件的恒力。

如图是位于锦江乐园的摩天轮，高度为108$m$，直径是98$m$。一质量为50$kg$的游客乘坐该摩天轮做匀速圆周运动旋转一圈需25$min$。如果以地面为零势能面，则他到达最高处时的（取$g$=10$m/s^2$）（）。

降落伞在匀速下降过程中遇到水平方向吹来的风，若风速越大，则降落伞（）

月球绕地球做匀速圆周运动的向心加速度大小为$a$，设月球表面的重力加速度大小为$g_1$，在月球绕地球运行的轨道处由地球引力产生的加速度大小为$g_2$，则（）

如图，三个质点$a$、$b$、$c$质量分别为$m_1$、$m_2$、$M$（$M\gg m_1,M\gg m_2$）.在C的万有引力作用下，$a$、$b$在同一平面内绕$c$沿逆时针方向做匀速圆周运动，轨道半径之比$r_a:r_b=1:4$,则它们的周期之比$T_a:T_b=$;从图示位置开始，在$b$运动一周的过程中，$a$、$b$、$c$共线了次。

如图，$ABC$和$ABD$为两个光滑固定轨道，$A$、$B$、$E$在同一水平面，$C$、$D$、$E$在同一竖直线上，$D$点距水平面的高度$h$，$C$点高度为$2h$，一滑块从$A$点以初速度$v_0$分别沿两轨道滑行到$C$或$D$处后水平抛出。

（1）求滑块落到水平面时，落点与$E$点间的距离$s_C$和$s_D$

（2）为实现$s_C<s_D$，$v_0$应满足什么条件？

一水平抛出的小球落到一倾角为_$\theta$的斜面上时，其速度方向与斜面垂直，运动轨迹如右图中虚线所示。小球在竖直方向下落的距离与在水平方向通过的距离之比为