2022年中考数学专题:一次函数
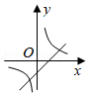
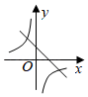
函数 的图象如图所示,则关于 的一元二次方程 的根的情况是
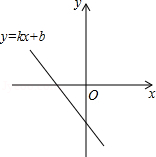
| A. |
没有实数根 |
B. |
有两个相等的实数根 |
| C. |
有两个不相等的实数根 |
D. |
无法确定 |
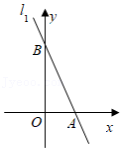
数形结合是解决数学问题常用的思想方法.如图,直线 与直线 相交于点 .根据图象可知,关于 的不等式 的解集是
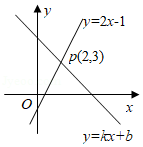
| A. |
|
B. |
|
C. |
|
D. |
|
某物体在力 的作用下,沿力的方向移动的距离为 ,力对物体所做的功 与 的对应关系如图所示,则下列结论正确的是
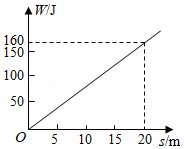
| A. |
|
B. |
|
C. |
|
D. |
|
已知一次函数 过点 ,则下列结论正确的是
| A. |
随 增大而增大 |
| B. |
|
| C. |
直线过点 |
| D. |
与坐标轴围成的三角形面积为2 |
甲无人机从地面起飞,乙无人机从距离地面 高的楼顶起飞,两架无人机同时匀速上升 .甲、乙两架无人机所在的位置距离地面的高度 (单位: 与无人机上升的时间 (单位: 之间的关系如图所示.下列说法正确的是
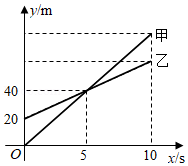
| A. |
时,两架无人机都上升了 |
| B. |
时,两架无人机的高度差为 |
| C. |
乙无人机上升的速度为 |
| D. |
时,甲无人机距离地面的高度是 |
如图,一次函数 的图象与 轴、 轴分别交于点 , ,把直线 绕点 顺时针旋转 交 轴于点 ,则线段 长为
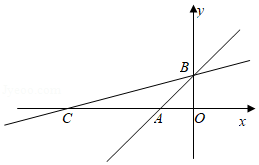
| A. |
|
B. |
|
C. |
|
D. |
|
定义:一次函数 的特征数为 , ,若一次函数 的图象向上平移3个单位长度后与反比例函数 的图象交于 , 两点,且点 , 关于原点对称,则一次函数 的特征数是
| A. |
, |
B. |
, |
C. |
, |
D. |
, |
为庆祝"中国共产党的百年华诞",某校请广告公司为其制作"童心向党"文艺活动的展板、宣传册和横幅,其中制作宣传册的数量是展板数量的5倍,广告公司制作每件产品所需时间和利润如表:
产品 |
展板 |
宣传册 |
横幅 |
制作一件产品所需时间(小时) |
1 |
|
|
制作一件产品所获利润(元 |
20 |
3 |
10 |
(1)若制作三种产品共计需要25小时,所获利润为450元,求制作展板、宣传册和横幅的数量;
(2)若广告公司所获利润为700元,且三种产品均有制作,求制作三种产品总量的最小值.
如图,一次函数 的图象与反比例函数 的图象相交,其中一个交点的横坐标是1.
(1)求 的值;
(2)若将一次函数 的图象向下平移4个单位长度,平移后所得到的图象与反比例函数 的图象相交于 , 两点,求此时线段 的长.
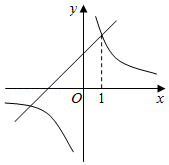
黔东南州某销售公司准备购进 、 两种商品,已知购进3件 商品和2件 商品,需要1100元;购进5件 商品和3件 商品,需要1750元.
(1)求 、 两种商品的进货单价分别是多少元?
(2)若该公司购进 商品200件, 商品300件,准备把这些商品全部运往甲、乙两地销售.已知每件 商品运往甲、乙两地的运费分别为20元和25元;每件 商品运往甲、乙两地的运费分别为15元和24元.若运往甲地的商品共240件,运往乙地的商品共260件.
①设运往甲地的 商品为 (件 ,投资总运费为 (元 ,请写出 与 的函数关系式;
②怎样调运 、 两种商品可使投资总费用最少?最少费用是多少元?(投资总费用 购进商品的费用 运费)
《九章算术》中记载,浮箭漏(图① 出现于汉武帝时期,它由供水壶和箭壶组成,箭壶内装有箭尺,水匀速地从供水壶流到箭壶,箭壶中的水位逐渐上升,箭尺匀速上浮,可通过读取箭尺读数计算时间.某学校 小组仿制了一套浮箭漏,并从函数角度进行了如下实验探究:
【实验观察】实验小组通过观察,每2小时记录一次箭尺读数,得到如表:
供水时间 (小时) |
0 |
2 |
4 |
6 |
8 |
箭尺读数 (厘米) |
6 |
18 |
30 |
42 |
54 |
【探索发现】①建立平面直角坐标系,如图②,横轴表示供水时间 .纵轴表示箭尺读数 ,描出以表格中数据为坐标的各点.
②观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由.
【结论应用】应用上述发现的规律估算:
①供水时间达到12小时时,箭尺的读数为多少厘米?
②如果本次实验记录的开始时间是上午 ,那当箭尺读数为90厘米时是几点钟?(箭尺最大读数为100厘米)
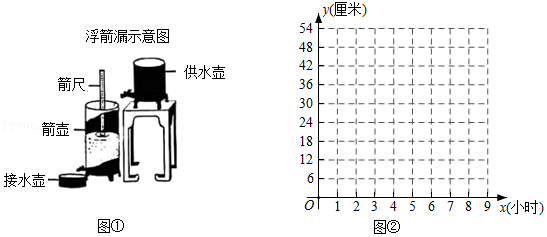
如图,直线 与双曲线 相交于点 、 ,已知点 的横坐标为1.
(1)求直线 的解析式及点 的坐标;
(2)以线段 为斜边在直线 的上方作等腰直角三角形 .求经过点 的双曲线的解析式.

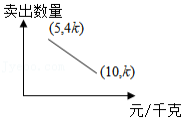
超市购进某种苹果,如果进价增加2元 千克要用300元;如果进价减少2元 千克,同样数量的苹果只用200元.
(1)求苹果的进价;
(2)如果购进这种苹果不超过100千克,就按原价购进;如果购进苹果超过100千克,超过部分购进价格减少2元 千克,写出购进苹果的支出 (元 与购进数量 (千克)之间的函数关系式;
(3)超市一天购进苹果数量不超过300千克,且购进苹果当天全部销售完,据统计,销售单价 (元 千克)与一天销售数量 (千克)的关系为 .在(2)的条件下,要使超市销售苹果利润 (元 最大,求一天购进苹果数量.(利润 销售收入 购进支出)
如图是某机场监控屏显示两飞机的飞行图象,1号指挥机(看成点 始终以 的速度在离地面 高的上空匀速向右飞行,2号试飞机(看成点 一直保持在1号机 的正下方.2号机从原点 处沿 仰角爬升,到 高的 处便立刻转为水平飞行,再过 到达 处开始沿直线 降落,要求 后到达 处.
(1)求 的 关于 的函数解析式,并直接写出2号机的爬升速度;
(2)求 的 关于 的函数解析式,并预计2号机着陆点的坐标;
(3)通过计算说明两机距离 不超过 的时长是多少.
注:(1)及(2)中不必写 的取值范围

学习了图形的旋转之后,小明知道,将点 绕着某定点 顺时针旋转一定的角度 ,能得到一个新的点 ,经过进一步探究,小明发现,当上述点 在某函数图象上运动时,点 也随之运动,并且点 的运动轨迹能形成一个新的图形.
试根据下列各题中所给的定点 的坐标、角度 的大小来解决相关问题.
【初步感知】
如图1,设 , ,点 是一次函数 图象上的动点,已知该一次函数的图象经过点 .
(1)点 旋转后,得到的点 的坐标为 ;
(2)若点 的运动轨迹经过点 ,求原一次函数的表达式.
【深入感悟】
如图2,设 , ,点 是反比例函数 的图象上的动点,过点 作二、四象限角平分线的垂线,垂足为 ,求 的面积.
【灵活运用】
如图3,设 , ,点 是二次函数 图象上的动点,已知点 、 ,试探究 的面积是否有最小值?若有,求出该最小值;若没有,请说明理由.
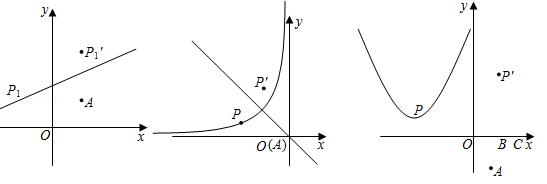
在"看图说故事"活动中,某学习小组结合图象设计了一个问题情境.已知学校、书店、陈列馆依次在同一条直线上,书店离学校 ,陈列馆离学校 .李华从学校出发,匀速骑行 到达书店;在书店停留 后,匀速骑行 到达陈列馆;在陈列馆参观学习一段时间,然后回学校;回学校途中,匀速骑行 后减速,继续匀速骑行回到学校.给出的图象反映了这个过程中李华离学校的距离 与离开学校的时间 之间的对应关系.
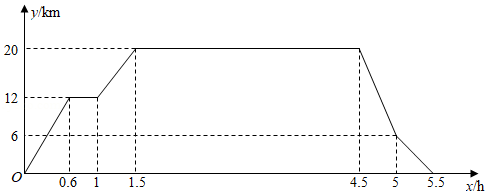
请根据相关信息,解答下列问题:
(Ⅰ)填表:
离开学校的时间 |
0.1 |
0.5 |
0.8 |
1 |
3 |
离学校的距离 |
2 |
10 |
|
12 |
|
(Ⅱ)填空:
①书店到陈列馆的距离为 ;
②李华在陈列馆参观学习的时间为 ;
③李华从陈列馆回学校途中,减速前的骑行速度为 ;
④当李华离学校的距离为 时,他离开学校的时间为 .
(Ⅲ)当 时,请直接写出 关于 的函数解析式.


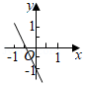







 粤公网安备 44130202000953号
粤公网安备 44130202000953号