2020年浙江省台州市中考数学试卷
在一次数学测试中,小明成绩72分,超过班级半数同学的成绩,分析得出这个结论所用的统计量是
A.中位数B.众数C.平均数D.方差
如图,已知线段 ,分别以 , 为圆心,大于 同样长为半径画弧,两弧交于点 , ,连接 , , , , ,则下列说法错误的是

A. 平分 B. 平分 C. D.
下列是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形.下列推理过程正确的是
A.由②推出③,由③推出①B.由①推出②,由②推出③
C.由③推出①,由①推出②D.由①推出③,由③推出②
如图1,小球从左侧的斜坡滚下,到达底端后又沿着右侧斜坡向上滚,在这个过程中,小球的运动速度 (单位: 与运动时间 (单位: 的函数图象如图2,则该小球的运动路程 (单位: 与运动时间 (单位: 之间的函数图象大致是

A. B.
B.
C. D.
D.
把一张宽为 的长方形纸片 折叠成如图所示的阴影图案,顶点 , 互相重合,中间空白部分是以 为直角顶点,腰长为 的等腰直角三角形,则纸片的长 (单位: 为

A. B. C. D.
如图,等边三角形纸片 的边长为6, , 是边 上的三等分点.分别过点 , 沿着平行于 , 方向各剪一刀,则剪下的 的周长是 .

甲、乙两位同学在10次定点投篮训练中(每次训练投8个),各次训练成绩(投中个数)的折线统计图如图所示,他们成绩的方差分别为 与 ,则 .(填“ ”、“ ”、“ ”中的一个)

用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖面积为 ,小正方形地砖面积为 ,依次连接四块大正方形地砖的中心得到正方形 .则正方形 的面积为 .(用含 , 的代数式表示)

人字折叠梯完全打开后如图1所示, , 是折叠梯的两个着地点, 是折叠梯最高级踏板的固定点.图2是它的示意图, , , ,求点 离地面的高度 .(结果精确到 ;参考数据 , , ,

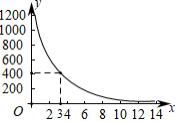
小明同学训练某种运算技能,每次训练完成相同数量的题目,各次训练题目难度相当.当训练次数不超过15次时,完成一次训练所需要的时间 (单位:秒)与训练次数 (单位:次)之间满足如图所示的反比例函数关系.完成第3次训练所需时间为400秒.
(1)求 与 之间的函数关系式;
(2)当 的值为6,8,10时,对应的函数值分别为 , , ,比较 与 的大小: .
新冠疫情期间,某校开展线上教学,有“录播”和“直播”两种教学方式供学生选择其中一种.为分析该校学生线上学习情况,在接受这两种教学方式的学生中各随机抽取40人调查学习参与度,数据整理结果如表(数据分组包含左端值不包含右端值).
参与度 人数 方式 |
|
|
|
|
录播 |
4 |
16 |
12 |
8 |
直播 |
2 |
10 |
16 |
12 |
(1)你认为哪种教学方式学生的参与度更高?简要说明理由.
(2)从教学方式为“直播”的学生中任意抽取一位学生,估计该学生的参与度在0.8及以上的概率是多少?
(3)该校共有800名学生,选择“录播”和“直播”的人数之比为 ,估计参与度在0.4以下的共有多少人?
如图,在 中, ,将 沿直线 翻折得到 ,连接 交 于点 . 是线段 上的点,连接 . 是 的外接圆与 的另一个交点,连接 , .
(1)求证: 是直角三角形;
(2)求证: ;
(3)当 , 时,在线段 上存在点 ,使得 和 互相平分,求 的值.

用各种盛水容器可以制作精致的家用流水景观(如图 .
科学原理:如图2,始终盛满水的圆柱体水桶水面离地面的高度为 (单位: ,如果在离水面竖直距离为 (单位: 的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离) (单位: 与 的关系式为 .

应用思考:现用高度为 的圆柱体塑料水瓶做相关研究,水瓶直立地面,通过连续注水保证它始终盛满水,在离水面竖直距离 处开一个小孔.
(1)写出 与 的关系式;并求出当 为何值时,射程 有最大值,最大射程是多少?
(2)在侧面开两个小孔,这两个小孔离水面的竖直距离分别为 , ,要使两孔射出水的射程相同,求 , 之间的关系式;
(3)如果想通过垫高塑料水瓶,使射出水的最大射程增加 ,求垫高的高度及小孔离水面的竖直距离.

 B.
B. C.
C. D.
D.

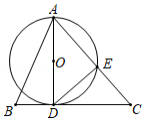

 粤公网安备 44130202000953号
粤公网安备 44130202000953号