2020年四川省自贡市中考数学试卷
5月22日晚,中国自贡第26届国际恐龙灯会开启网络直播,有着近千年历史的自贡灯会进入“云游”时代,70余万人通过“云观灯”感受了“天下第一灯”的璀璨.人数700000用科学记数法表示为
A. B. C. D.
某工程队承接了80万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了 ,结果提前40天完成了这一任务.设实际工作时每天绿化的面积为 万平方米,则下面所列方程中正确的是
A. B.
C. D.
如图,在平行四边形 中, , , 是锐角, 于点 , 是 的中点,连结 、 .若 ,则 长为

A.2B. C. D.
某中学新建食堂正式投入使用,为提高服务质量,食堂管理人员对学生进行了“最受欢迎菜品”的调查统计.以下是打乱了的调查统计顺序,请按正确顺序重新排序(只填番号) .
①绘制扇形图;
②收集最受学生欢迎菜品的数据;
③利用扇形图分析出最受学生欢迎的菜品;
④整理所收集的数据.
如图,我市在建高铁的某段路基横断面为梯形 , . 长6米,坡角 为 , 的坡角 为 ,则 长为 米(结果保留根号).

如图,矩形 中, 是 上一点,连接 ,将 沿 翻折,恰好使点 落在 边的中点 处,在 上取点 ,以 为圆心, 长为半径作半圆与 相切于点 .若 ,则图中阴影部分的面积为 .

如图,直线 与 轴交于点 ,与双曲线 在第三象限交于 、 两点,且 .下列等边三角形△ ,△ ,△ , 的边 , , , 在 轴上,顶点 , , , 在该双曲线第一象限的分支上,则 ,前25个等边三角形的周长之和为 .
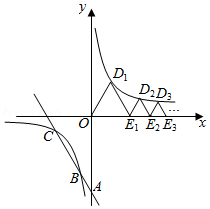
某校为了响应市政府号召,在“创文创卫”活动周中,设置了“ :文明礼仪, :环境保护, :卫生保洁, :垃圾分类”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如图条形统计图和扇形统计图.

(1)本次调查的学生人数是 人, ;
(2)请补全条形统计图;
(3)学校要求每位同学从星期一至星期五选择两天参加活动.如果小张同学随机选择连续两天,其中有一天是星期一的概率是 ;小李同学星期五要参加市演讲比赛,他在其余四天中随机选择两天,其中有一天是星期三的概率是 .
甲、乙两家商场平时以同样价格出售相同的商品.新冠疫情期间,为了减少库存,甲、乙两家商场打折促销.甲商场所有商品按9折出售,乙商场对一次购物中超过100元后的价格部分打8折.
(1)以 (单位:元)表示商品原价, (单位:元)表示实际购物金额,分别就两家商场的让利方式写出 关于 的函数解析式;
(2)新冠疫情期间如何选择这两家商场去购物更省钱?
我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”,数形结合是解决数学问题的重要思想方法.例如,代数式 的几何意义是数轴上 所对应的点与2所对应的点之间的距离:因为 ,所以 的几何意义就是数轴上 所对应的点与 所对应的点之间的距离.
(1)发现问题:代数式 的最小值是多少?
(2)探究问题:如图,点 、 、 分别表示数 、2、 , .
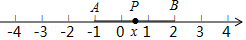
的几何意义是线段 与 的长度之和,
当点 在线段 上时, ,当点 在点 的左侧或点 的右侧时, .
的最小值是3.
(3)解决问题:
① 的最小值是 ;
②利用上述思想方法解不等式: ;
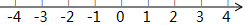
③当 为何值时,代数式 的最小值是2.
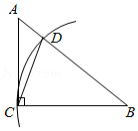
如图, 是 的外接圆, 为直径,点 为 外一点,且 ,连接 交 于点 ,延长 交 于点 .
(1)证明: ;
(2)若 ,证明: 是 的切线;
(3)在(2)条件下,连接 交 于点 ,连接 ,若 ,求 的长.



 B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.
 B.
B.
 D.
D.


 粤公网安备 44130202000953号
粤公网安备 44130202000953号