2018年福建省中考数学试卷(A卷)
下列各组数中,能作为一个三角形三边边长的是
| A. |
1,1,2 |
B. |
1,2,4 |
C. |
2,3,4 |
D. |
2,3,5 |
投掷两枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,则下列事件为随机事件的是
| A. |
两枚骰子向上一面的点数之和大于1 |
| B. |
两枚骰子向上一面的点数之和等于1 |
| C. |
两枚骰子向上一面的点数之和大于12 |
| D. |
两枚骰子向上一面的点数之和等于12 |
我国古代数学著作《增删算法统宗》记载"绳索量竿"问题:"一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托."其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长 尺,竿长 尺,则符合题意的方程组是
| A. |
|
B. |
|
| C. |
|
D. |
|
已知关于 的一元二次方程 有两个相等的实数根,下列判断正确的是
| A. |
1一定不是关于 的方程 的根 |
| B. |
0一定不是关于 的方程 的根 |
| C. |
1和 都是关于 的方程 的根 |
| D. |
1和 不都是关于 的方程 的根 |
某8种食品所含的热量值分别为:120,134,120,119,126,120,118,124,则这组数据的众数为 .
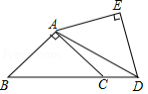
把两个同样大小的含 角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点 ,且另三个锐角顶点 , , 在同一直线上.若 ,则 .
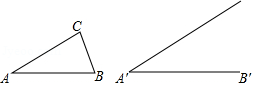
求证:相似三角形对应边上的中线之比等于相似比.
要求:①根据给出的 及线段 , ,以线段 为一边,在给出的图形上用尺规作出△ ,使得△ ,不写作法,保留作图痕迹;
②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.
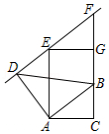
如图,在 中, , , .线段 由线段 绕点 按逆时针方向旋转 得到, 由 沿 方向平移得到,且直线 过点 .
(1)求 的大小;
(2)求 的长.
甲、乙两家快递公司揽件员(揽收快件的员工)的日工资方案如下:
甲公司为"基本工资 揽件提成",其中基本工资为70元 日,每揽收一件提成2元;
乙公司无基本工资,仅以揽件提成计算工资.若当日揽件数不超过40,每件提成4元;若当日搅件数超过40,超过部分每件多提成2元.
如图是今年四月份甲公司揽件员人均揽件数和乙公司揽件员人均揽件数的条形统计图:
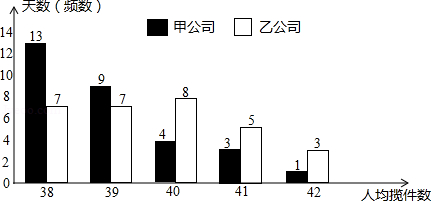
(1)现从今年四月份的30天中随机抽取1天,求这一天甲公司揽件员人均揽件数超过40(不含40)的概率;
(2)根据以上信息,以今年四月份的数据为依据,并将各公司揽件员的人均揽件数视为该公司各揽件员的揽件数,解决以下问题:
①估计甲公司各揽件员的日平均揽件数;
②小明拟到甲、乙两家公司中的一家应聘揽件员,如果仅从工资收入的角度考虑,请利用所学的统计知识帮他选择,并说明理由.
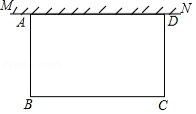
如图,在足够大的空地上有一段长为 米的旧墙 ,某人利用旧墙和木栏围成一个矩形菜园 ,其中 ,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若 ,所围成的矩形菜园的面积为450平方米,求所利用旧墙 的长;
(2)求矩形菜园 面积的最大值.
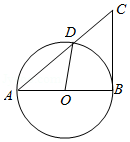
已知四边形 是 的内接四边形, 是 的直径, ,垂足为 .
(1)延长 交 于点 ,延长 , 交于点 ,如图1.求证: ;
(2)过点 作 ,垂足为 , 交 于点 ,且点 和点 都在 的左侧,如图2.若 , , ,求 的大小.





 粤公网安备 44130202000953号
粤公网安备 44130202000953号