2017年江苏省扬州市中考数学试卷
在一列数: , , , , 中, , ,从第三个数开始,每一个数都等于它前两个数之积的个位数字,则这一列数中的第2017个数是
A.1B.3C.7D.9
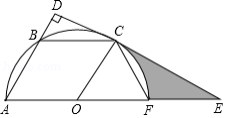
如图,已知 的顶点坐标分别为 、 、 ,若二次函数 的图象与阴影部分(含边界)一定有公共点,则实数 的取值范围是
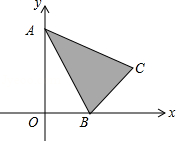
A. B. C. D.
2017年5月18日,我国在南海北部神弧海域进行的可燃冰试开采成功,标志着我国成为全球第一个在海域可燃冰开采中获得连续稳定的国家.目前每日的天然气试开采量约为16000立方米,把16000立方米用科学记数法表示为 立方米.
为了了解某班数学成绩情况,抽样调查了13份试卷成绩,结果如下:3个140分,4个135分,2个130分,2个120分,1个100分,1个80分.则这组数据的中位数为 分.
同一温度的华氏度数 与摄氏度数 之间的函数表达式是 .若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为 .
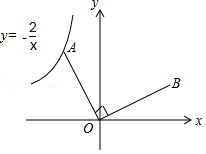
如图,已知点 是反比例函数 的图象上的一个动点,连接 ,若将线段 绕点 顺时针旋转 得到线段 ,则点 所在的反比例函数表达式为 .
“富春包子”是扬州特色早点,富春茶社为了了解顾客对各种早点的喜爱情况,设计了如右图的调查问卷,对顾客进行了抽样调查.根据统计数据绘制了如下尚不完整的统计图.
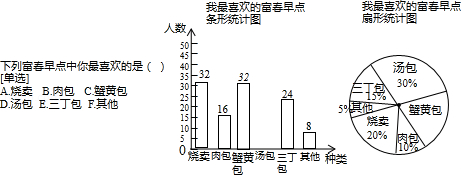
根据以上信息,解决下列问题:
(1)条形统计图中“汤包”的人数是 ,扇形统计图中“蟹黄包”部分的圆心角为 ;
(2)根据抽样调查结果,请你估计富春茶社1000名顾客中喜欢“汤包”的有多少人?
车辆经过润扬大桥收费站时,4个收费通道 、 、 、 中,可随机选择其中的一个通过.
(1)一辆车经过此收费站时,选择 通道通过的概率是 ;
(2)求两辆车经过此收费站时,选择不同通道通过的概率.
星期天,小明和小芳从同一小区门口同时出发,沿同一路线去离该小区1800米的少年宫参加活动,为响应“节能环保,绿色出行”的号召,两人都步行,已知小明的速度是小芳的速度的1.2倍,结果小明比小芳早6分钟到达,求小芳的速度.
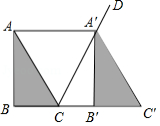
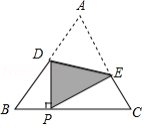
如图,将 沿着射线 方向平移至△ ,使点 落在 的外角平分线 上,连接 .
(1)判断四边形 的形状,并说明理由;
(2)在 中, , , ,求 的长.
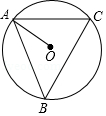
如图,已知平行四边形 的三个顶点 、 、 在以 为圆心的半圆上,过点 作 ,分别交 、 的延长线于点 、 , 交半圆 于点 ,连接 .
(1)判断直线 与半圆 的位置关系,并说明理由;
(2)①求证: ;
②若半圆 的半径为12,求阴影部分的周长.
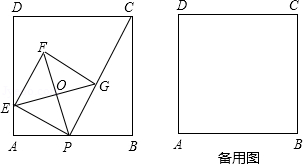
我们规定:三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差.如图1,在 中, 是 边上的中线, 与 的“极化值”就等于 的值,可记为 △ .
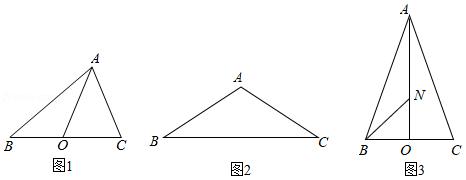
(1)在图1中,若 , , , 是 边上的中线,则 △ , △ ;
(2)如图2,在 中, , ,求 △ 、 △ 的值;
(3)如图3,在 中, , 是 边上的中线,点 在 上,且 .已知 △ , △ ,求 的面积.
农经公司以30元 千克的价格收购一批农产品进行销售,为了得到日销售量 (千克)与销售价格 (元 千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格 (元 千克) |
30 |
35 |
40 |
45 |
50 |
日销售量 (千克) |
600 |
450 |
300 |
150 |
0 |
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定 与 之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出 元 的相关费用,当 时,农经公司的日获利的最大值为2430元,求 的值.(日获利 日销售利润 日支出费用)
 B.
B. C.
C. D.
D.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号