2017年贵州省黔东南州中考数学试卷
如图,抛物线 的对称轴为直线 ,给出下列结论:
① ;② ;③ ;④ ,其中正确的个数有

A.1个B.2个C.3个D.4个
我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项式 的展开式的各项系数,此三角形称为“杨辉三角”.
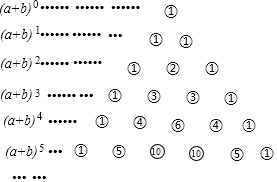
根据“杨辉三角”请计算 的展开式中第三项的系数为
A.2017B.2016C.191D.190
黔东南下司“蓝莓谷”以盛产“优质蓝莓”而吸引来自四面八方的游客,某果农今年的蓝莓得到了丰收,为了了解自家蓝莓的质量,随机从种植园中抽取适量蓝莓进行检测,发现在多次重复的抽取检测中“优质蓝莓”出现的频率逐渐稳定在0.7,该果农今年的蓝莓总产量约为 ,由此估计该果农今年的“优质蓝莓”产量约是 .
把多块大小不同的 直角三角板如图所示,摆放在平面直角坐标系中,第一块三角板 的一条直角边与 轴重合且点 的坐标为 , ;第二块三角板的斜边 与第一块三角板的斜边 垂直且交 轴于点 ;第三块三角板的斜边 与第二块三角板的斜边 垂直且交 轴于点 ;第四块三角板的斜边 与第三块三角板的斜边 垂直且交 轴于点 ; 按此规律继续下去,则点 的坐标为 .

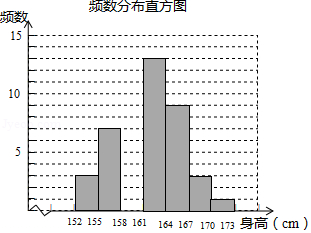
某体育老师测量了自己任教的甲、乙两班男生的身高,并制作了如下不完整的统计图表.
身高分组 |
频数 |
频率 |
|
3 |
0.06 |
|
7 |
0.14 |
|
|
0.28 |
|
13 |
|
|
9 |
0.18 |
|
3 |
0.06 |
|
1 |
0.02 |
根据以上统计图表完成下列问题:
(1)统计表中 , ,并将频数分布直方图补充完整;
(2)在这次测量中两班男生身高的中位数在: 范围内;
(3)在身高 的4人中,甲、乙两班各有2人,现从4人中随机推选2人补充到学校国旗护卫队中,请用列表或画树状图的方法求出这两人都来自相同班级的概率.
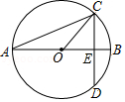
如图,已知直线 与 相切于点 ,直线 与 相交于 , 两点.
(1)求证: ;
(2)若 ,求图中阴影部分的面积.

如图,某校教学楼 后方有一斜坡,已知斜坡 的长为12米,坡角 为 ,根据有关部门的规定, 时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡 进行改造,在保持坡脚 不动的情况下,学校至少要把坡顶 向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据: , , , , ,

某校为了在九月份迎接高一年级的新生,决定将学生公寓楼重新装修.现学校招用了甲、乙两个工程队.若两队合作,8天就可以完成该项工程;若由甲队先单独做3天后,剩余部分由乙队单独做需要18天才能完成.
(1)求甲、乙两队工作效率分别是多少?
(2)甲队每天工资3000元,乙队每天工资1400元.学校要求在12天内将学生公寓楼装修完成.若完成该工程甲队工作 天,乙队工作 天.求学校需支付的总工资 (元 与甲队工作天数 (天 的函数关系式,并求出 的取值范围及 的最小值.






 粤公网安备 44130202000953号
粤公网安备 44130202000953号