2016年四川省凉山州中考数学试卷
如图, 是由若干个大小相同的正方体搭成的几何体的三视图, 该几何体所用的正方体的个数是

A . 6B . 4C . 3D . 2
一个多边形切去一个角后,形成的另一个多边形的内角和为 ,那么原多边形的边数为
A.7B.7或8C.8或9D.7或8或9
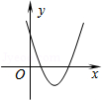
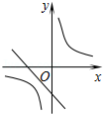
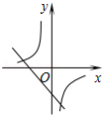
在线段、平行四边形、矩形、等腰三角形、圆这几个图形中既是轴对称图形又是中心对称图形的个数是
A.2个B.3个C.4个D.5个
教练要从甲、乙两名射击运动员中选一名成绩较稳定的运动员参加比赛.两人在形同条件下各打了5发子弹,命中环数如下:甲:9、8、7、7、9;乙:10、8、9、7、6.应该选 参加.
A.甲B.乙C.甲、乙都可以D.无法确定
观察图中正方形四个顶点所标的数字规律, 可知, 数 2016 应标在

A . 第 504 个正方形的左下角B . 第 504 个正方形的右下角
C . 第 505 个正方形的左上角D . 第 505 个正方形的右下角
为了切实关注、关爱贫困家庭学生,某校对全校各班贫困家庭学生的人数情况进行了统计,以便国家精准扶贫政策有效落实.统计发现班上贫困家庭学生人数分别有2名、3名、4名、5名、6名,共五种情况.并将其制成了如下两幅不完整的统计图:

(1)求该校一共有多少个班?并将条形图补充完整;
(2)某爱心人士决定从2名贫困家庭学生的这些班级中,任选两名进行帮扶,请用列表法或树状图的方法,求出被选中的两名学生来自同一班级的概率.
如图,在边长为1的正方形网格中, 的顶点均在格点上,点 、 的坐标分别是 、 ,把 绕点 逆时针旋转 后得到△ .
(1)画出△ ,直接写出点 、 的坐标;
(2)求在旋转过程中, 所扫过的面积.

在创建“全国文明城市”和“省级文明城区”过程中,栾城区污水处理厂决定先购买 、 两型污水处理设备共20台,对城区周边污水进行处理.已知每台 型设备价格为12万元,每台 型设备价格为10万元;1台 型设备和2台 型设备每周可以处理污水640吨,2台 型设备和3台 型设备每周可以处理污水1080吨.
(1)求 、 两型污水处理设备每周分别可以处理污水多少吨?
(2)要想使污水处理厂购买设备的资金不超过230万元,但每周处理污水的量又不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少?
阅读下列材料并回答问题:
材料1:如果一个三角形的三边长分别为 , , ,记 ,那么三角形的面积为 . ①
古希腊几何学家海伦 ,约公元50年),在数学史上以解决几何测量问题而闻名.他在《度量》一书中,给出了公式①和它的证明,这一公式称海伦公式.
我国南宋数学家秦九韶(约 约 ,曾提出利用三角形的三边求面积的秦九韶公式: . ②
下面我们对公式②进行变形: .
这说明海伦公式与秦九韶公式实质上是同一公式,所以我们也称①为海伦 秦九韶公式.
问题:如图,在 中, , , , 内切于 ,切点分别是 、 、 .
(1)求 的面积;
(2)求 的半径.

如图,已知四边形 内接于 , 是 的中点, 于 ,与 及 的延长线交于点 、 ,且 .
(1)求证: ;
(2)如果 , ,求 的值.


 B.
B.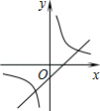
 D.
D.




 粤公网安备 44130202000953号
粤公网安备 44130202000953号