2019年内蒙古兴安盟中考数学试卷

在实数﹣3， $\sqrt{3}$ ，0，﹣1中，最小的数是（　　）

下列各式计算正确的是（　　）

点 A（4，﹣2）关于 x轴的对称点的坐标为（　　）

如图，已知 AB＝ AC，点 D、 E分别在线段 AB、 AC上， BE与 CD相交于点 O，添加以下哪个条件仍不能判定△ ABE≌△ ACD（　　）

一个多边形的内角和是外角和的2倍，这个多边形是（　　）

为了鼓励学生加强体育锻炼，学校在制定奖励方案前进行问卷调查，设置"赞成、反对、无所谓"三种意见，从全校2000名学生中随机抽取100名学生进行调查，其中持"反对"和"无所谓"意见的共有30名学生，估计全校持"赞成"意见的学生人数约为（　　）

已知：如图，是由若干个大小相同的小正方体所搭成的几何体的三视图，则搭成这个几何体的小正方体的个数是（　　）

下列命题正确的是（　　）

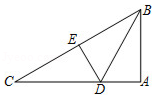
如图， BD是△ ABC的角平分线， DE是 BC的垂直平分线，∠ BAC＝90°， AD＝3，则 CD的长为（　　）

甲、乙两人分别从距目的地6千米和10千米的两地同时出发，乙的速度是甲的1.2倍，结果甲比乙早到20分钟．设甲的速度为 x千米/时．根据题意，列方程正确的是（　　）

如图，反比例函数 y＝ $\frac{2}{x}$ 的图象经过矩形 OABC的边 AB的中点 D，则矩形 OABC的面积为（　　）

如图，△ ABC中， AC＝ BC＝3， AB＝2，将它沿 AB翻折得到△ ABD，点 P、 E、 F分别为线段 AB、 AD、 DB上的动点，则 PE+ PF的最小值是（　　）

函数 y＝ $\frac{1}{\sqrt{x-3}}$ 自变量的取值范围是 　 ．

太阳的半径大约为696000千米，将696000用科学记数表示为 　　．

若抛物线 y＝﹣ x ²﹣6 x+ m与 x轴没有交点，则 m的取值范围是 　．

在Rt△ ABC中，∠ C＝90°， AC＝3， BC＝4，把它沿斜边 AB所在直线旋转一周，所得几何体的侧面积是 　　．（结果保留π）

下列图形都是由同样大小的菱形按照一定规律组成的，其中第①个图形中共有3个菱形，第②个图形中共有7个菱形，第③个图形中共有13个菱形……按此规律排列下去，第 　　个图形中菱形的个数为10101个．

计算： $\frac{1}{\sqrt{2}}$ ﹣| $\sqrt{2}$ ﹣2|+（1﹣cos45°）+（﹣ $\frac{1}{3}$ ） ^{﹣ 2}．

先化简，再求值： $\frac{x-3}{x^2-1}\cdot \frac{x^2+2x+1}{x-3}-\left(\frac{1}{x-1}+1\right)$ ，其中 x＝﹣6．

如图，海中有一个小岛 A，它周围8海里内有暗礁．渔船跟踪鱼群由西向东航行，在 B点测得小岛 A在北偏东60°方向上，航行10海里到达 C点，这时测得小岛 A在北偏东30°方向上．如果渔船不改变航线继续向东航行，有没有触礁的危险？

如图，有四张背面完全相同的纸牌 A、 B、 C、 D，其正面分别画有四个不同的几何图形，将这四张纸牌背面朝上洗匀．

（1）从中随机摸出一张，求摸出的牌面图形是中心对称图形的概率；

（2）小明和小亮约定做一个游戏，其规则为：先由小明随机摸出一张纸牌，不放回，再由小亮从剩下的纸牌中随机摸出一张，若摸出的两张牌面图形都是轴对称图形小明获胜，否则小亮获胜，这个游戏公平吗？请用列表法（或树状图）说明理由（纸牌用 A、 B、 C、 D表示）．

如图，在△ ABC中， BD、 CE分别是 AC、 AB上的中线， BD与 CE相交于点 O．

（1）利用尺规作图取线段 CO的中点．（保留作图痕迹，不写作法）；

（2）猜想 CO与 OE的长度有什么关系，并说明理由．

某商场统计了每个营业员在某月的销售额，绘制了如下统计图．

解答下列问题：

（1）设营业员的月销售额为 x（单位：万元）．商场规定：当 x＜15时为不称职，当15≤ x＜20时为基本称职，当20≤ x＜25时为称职，当 x≥25时为优秀．试求出基本称职、称职两个层次营业员人数所占百分比，并补全扇形图；

（2）根据（1）中规定，所有称职和优秀的营业员月销售额的中位数为 　　，众数为 　　；

（3）为了调动营业员的积极性，商场制定月销售额奖励标准，凡达到或超过这个标准的受到奖励．如果要使称职和优秀的营业员半数左右能获奖，奖励标准应定为多少万元？简述理由．

如图，△ ACE内接于⊙ O， AB是⊙ O的直径，弦 CD⊥ AB于点 H，交 AE于点 F，过点 E作 EG∥ AC，分别交 CD、 AB的延长线于点 G、 M．

（1）求证：△ ECF∽△ GCE；

（2）若tan G＝ $\frac{\text{3}}{\text{4}}$ ， AH＝3 $\sqrt{\text{3}}$ ，求⊙ O半径．

某书店在"读书节"之前，图书按标价销售，在"读书节"期间制定了活动计划．

（1）"读书节"之前小明发现：购买5本 A图书和8本 B图书共花279元，购买10本 A图书比购买6本 B图书多花162元，请求出 A、 B图书的标价；

（2）"读书节"期间书店计划用不超过3680元购进 A、 B图书共200本，且 A图书不少于50本， A、 B两种图书进价分别为24元、16元；销售时准备 A图书每本降价1.5元， B图书价格不变，那么书店如何进货才能使利润最大？

如图，在▱ OABC中， A、 C两点的坐标分别为（4，0）、（﹣2，3），抛物线 W经过 O、 A、 C三点，点 D是抛物线 W的顶点．

（1）求抛物线 W的函数解析式及顶点 D的坐标；

（2）将抛物线 W和▱ OABC同时先向右平移4个单位长度，再向下平移 m（0＜ m＜3）个单位长度，得到抛物线 W ₁和□ O ₁ A ₁ B ₁ C ₁，在向下平移过程中， O ₁ C ₁与 x轴交于点 H，▱ O ₁ A ₁ B ₁ C ₁与▱ OABC重叠部分的面积记为 S，试探究：当 m为何值时， S有最大值，并求出 S的最大值；

（3）在（2）的条件下，当 S取最大值时，设此时抛物线 W ₁的顶点为 F，若点 M是 x轴上的动点，点 N是抛物线 W ₁上的动点，是否存在这样的点 M、 N，使以 D、 F、 M、 N为顶点的四边形是平行四边形？若存在，求出点 M的坐标；若不存在，请说明理由．