2019年内蒙古包头市中考数学试卷

计算|﹣ $\sqrt{\text{3}}$ |+（ $\frac{\text{1}}{\text{3}}$ ） ^{﹣ 1}的结果是（　　）

实数 a， b在数轴上的对应点的位置如图所示．下列结论正确的是（　　）

一组数据2，3，5， x，7，4，6，9的众数是4，则这组数据的中位数是（　　）

一个圆柱的三视图如图所示，若其俯视图为圆，则这个圆柱的体积为（　　）

在函数 y＝ $\frac{\text{3}}{x-2}$ ﹣ $\sqrt{x+1}$ 中，自变量 x的取值范围是（　　）

下列说法正确的是（　　）

如图，在Rt△ ABC中，∠ B＝90°，以点 A为圆心，适当长为半径画弧，分别交 AB、 AC于点 D， E，再分别以点 D、 E为圆心，大于 $\frac{1}{2}$ DE为半径画弧，两弧交于点 F，作射线 AF交边 BC于点 G，若 BG＝1， AC＝4，则△ ACG的面积是（　　）

如图，在Rt△ ABC中，∠ ACB＝90°， AC＝ BC＝2 $\mathrm{}\sqrt{2}$ ，以 BC为直径作半圆，交 AB于点 D，则阴影部分的面积是（　　）

下列命题：

①若 x ²+ kx+ $\mathrm{}\frac{1}{4}$ 是完全平方式，则 k＝1；

②若 A（2，6）， B（0，4）， P（1， m）三点在同一直线上，则 m＝5；

③等腰三角形一边上的中线所在的直线是它的对称轴；

④一个多边形的内角和是它的外角和的2倍，则这个多边形是六边形．

其中真命题个数是（　　）

已知等腰三角形的三边长分别为 a、 b、4，且 a、 b是关于 x的一元二次方程 x ²﹣12 x+ m+2＝0的两根，则 m的值是（　　）

如图，在正方形 ABCD中， AB＝1，点 E， F分别在边 BC和 CD上， AE＝ AF，∠ EAF＝60°，则 CF的长是（　　）

如图，在平面直角坐标系中，已知 A（﹣3，﹣2）， B（0，﹣2）， C（﹣3，0）， M是线段 AB上的一个动点，连接 CM，过点 M作 MN⊥ MC交 y轴于点 N，若点 M、 N在直线 y＝ kx+ b上，则 b的最大值是（　　）

2018年我国国内生产总值（ GDP）是900309亿元，首次突破90万亿大关，90万亿用科学记数法表示为 　　．

已知不等式组 $\left\{\begin{array}{c}2x+9>-6x+1\\ x-k>1\end{array}\right.$ 的解集为 x＞﹣1，则 k的取值范围是 　　．

化简： $1-\frac{a-1}{a+2}÷\frac{a^2-1}{a^2+4a+4}$ ＝ 　　．

甲、乙两班举行数学知识竞赛，参赛学生的竞赛得分统计结果如下表：

某同学分析上表后得到如下结论：

①甲、乙两班学生的平均成绩相同；

②乙班优秀的人数少于甲班优秀的人数（竞赛得分≥85分为优秀）；

③甲班成绩的波动性比乙班小．

上述结论中正确的是 　　．（填写所有正确结论的序号）

如图，在△ ABC中，∠ CAB＝55°，∠ ABC＝25°，在同一平面内，将△ ABC绕 A点逆时针旋转70°得到△ ADE，连接 EC，则tan∠ DEC的值是 　　．

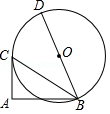
如图， BD是⊙ O的直径， A是⊙ O外一点，点 C在⊙ O上， AC与⊙ O相切于点 C，∠ CAB＝90°，若 BD＝6， AB＝4，∠ ABC＝∠ CBD，则弦 BC的长为 　　．

如图，在平面直角坐标系中，已知 A（﹣1，0）， B（0，2），将△ ABO沿直线 AB翻折后得到△ ABC，若反比例函数 y＝ $\frac{k}{x}$ （ x＜0）的图象经过点 C，则 k＝ 　　．

如图，在Rt△ ABC中，∠ ABC＝90°， BC＝3， D为斜边 AC的中点，连接 BD，点 F是 BC边上的动点（不与点 B、 C重合），过点 B作 BE⊥ BD交 DF延长线交于点 E，连接 CE，下列结论：

①若 BF＝ CF，则 CE ²+ AD ²＝ DE ²；

②若∠ BDE＝∠ BAC， AB＝4，则 CE＝ $\frac{15}{8}$ ；

③△ ABD和△ CBE一定相似；

④若∠ A＝30°，∠ BCE＝90°，则 DE＝ $\sqrt{21}$ ．

其中正确的是 　．（填写所有正确结论的序号）

某校为了解九年级学生的体育达标情况，随机抽取50名九年级学生进行体育达标项目测试，测试成绩如下表，请根据表中的信息，解答下列问题：

（1）该校九年级有450名学生，估计体育测试成绩为25分的学生人数；

（2）该校体育老师要对本次抽测成绩为23分的甲、乙、丙、丁4名学生进行分组强化训练，要求两人一组，求甲和乙恰好分在同一组的概率．（用列表或树状图方法解答）

如图，在四边形 ABCD中， AD∥ BC， AB＝ BC，∠ BAD＝90°， AC交 BD于点 E，∠ ABD＝30°， AD＝ $\sqrt{3}$ ，求线段 AC和 BE的长．

（注： $\frac{1}{\sqrt{a}+\sqrt{b}}=\frac{\sqrt{a}-\sqrt{b}}{(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})}=\frac{\sqrt{a}-\sqrt{b}}{a-b}$ ）

某出租公司有若干辆同一型号的货车对外出租，每辆货车的日租金实行淡季、旺季两种价格标准，旺季每辆货车的日租金比淡季上涨 $\frac{1}{3}$ ．据统计，淡季该公司平均每天有10辆货车未出租，日租金总收入为1500元；旺季所有的货车每天能全部租出，日租金总收入为4000元．

（1）该出租公司这批对外出租的货车共有多少辆？淡季每辆货车的日租金多少元？

（2）经市场调查发现，在旺季如果每辆货车的日租金每上涨20元，每天租出去的货车就会减少1辆，不考虑其它因素，每辆货车的日租金上涨多少元时，该出租公司的日租金总收入最高？

如图，在⊙ O中， B是⊙ O上的一点，∠ ABC＝120°，弦 AC＝2 $\mathrm{}\sqrt{3}$ ，弦 BM平分∠ ABC交 AC于点 D，连接 MA， MC．

（1）求⊙ O半径的长；

（2）求证： AB+ BC＝ BM．

如图，在正方形 ABCD中， AB＝6， M是对角线 BD上的一个动点（0＜ DM＜ $\frac{1}{2}$ BD），连接 AM，过点 M作 MN⊥ AM交 BC于点 N．

（1）如图①，求证： MA＝ MN；

（2）如图②，连接 AN， O为 AN的中点， MO的延长线交边 AB于点 P，当 $\frac{S_{△\mathit{AMN}}}{S_{△\mathit{BCD}}}=\frac{13}{18}$ 时，求 AN和 PM的长；

（3）如图③，过点 N作 NH⊥ BD于 H，当 AM＝2 $\mathrm{}\sqrt{5}$ 时，求△ HMN的面积．

如图，在平面直角坐标系中，已知抛物线 y＝ ax ²+ bx+2（ a≠0）与 x轴交于 A（﹣1，0）， B（3，0）两点，与 y轴交于点 C，连接 BC．

（1）求该抛物线的解析式，并写出它的对称轴；

（2）点 D为抛物线对称轴上一点，连接 CD、 BD，若∠ DCB＝∠ CBD，求点 D的坐标；

（3）已知 F（1，1），若 E（ x， y）是抛物线上一个动点（其中1＜ x＜2），连接 CE、 CF、 EF，求△ CEF面积的最大值及此时点 E的坐标．

（4）若点 N为抛物线对称轴上一点，抛物线上是否存在点 M，使得以 B， C， M， N为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点 M的坐标；若不存在，请说明理由．