2020年广东省深圳市中考数学试卷
2020年6月30日,深圳市总工会启动"百万职工消费扶贫采购节"活动,预计撬动扶贫消费额约150000000元.将150000000用科学记数法表示为
| A. |
|
B. |
|
C. |
|
D. |
|
某同学在今年的中考体育测试中选考跳绳.考前一周,他记录了自己五次跳绳的成绩(次数 分钟) ,253,247,255,263.这五次成绩的平均数和中位数分别是
| A. |
253,253 |
B. |
255,253 |
C. |
253,247 |
D. |
255,247 |
如图,在 中, .在 、 上分别截取 , ,使 .再分别以点 , 为圆心,以大于 的长为半径作弧,两弧在 内交于点 ,作射线 ,交 于点 .若 ,则 的长为

| A. |
2 |
B. |
3 |
C. |
4 |
D. |
5 |
以下说法正确的是
| A. |
平行四边形的对边相等 |
| B. |
圆周角等于圆心角的一半 |
| C. |
分式方程 的解为 |
| D. |
三角形的一个外角等于两个内角的和 |
如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的 、 两点分别测定对岸一棵树 的位置, 在 的正北方向,且 在 的北偏西 方向,则河宽 的长)可以表示为

| A. |
米 |
B. |
米 |
C. |
米 |
D. |
米 |
如图,矩形纸片 中, , .将纸片折叠,使点 落在边 的延长线上的点 处,折痕为 ,点 、 分别在边 和边 上.连接 ,交 于点 , 交 于点 .给出以下结论:
① ;
② ;
③ 和 的面积相等;
④当点 与点 重合时, ,
其中正确的结论共有

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
一口袋内装有编号分别为1,2,3,4,5,6,7的七个球(除编号外都相同),从中随机摸出一个球,则摸出编号为偶数的球的概率是 .
以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展,新业态发展对人才的需求更加旺盛.某大型科技公司上半年新招聘软件、硬件、总线、测试四类专业的毕业生,现随机调查了 名新聘毕业生的专业情况,并将调查结果绘制成如图两幅不完整的统计图.

请根据统计图提供的信息,解答下列问题.
(1) , .
(2)请补全条形统计图;
(3)在扇形统计图中,"软件"所对应的扇形的圆心角是 度;
(4)若该公司新招聘600名毕业生,请你估计"总线"专业的毕业生有 名.
如图, 为 的直径,点 在 上, 与过点 的切线互相垂直,垂足为 .连接 并延长,交 的延长线于点 .
(1)求证: ;
(2)若 , ,求 的长.

端午节前夕,某商铺用620元购进50个肉粽和30个蜜枣粽,肉粽的进货单价比蜜枣粽的进货单价多6元.
(1)肉粽和蜜枣粽的进货单价分别是多少元?
(2)由于粽子畅销,商铺决定再购进这两种粽子共300个,其中肉粽数量不多于蜜枣粽数量的2倍,且每种粽子的进货单价保持不变,若肉粽的销售单价为14元,蜜枣粽的销售单价为6元,试问第二批购进肉粽多少个时,全部售完后,第二批粽子获得利润最大?第二批粽子的最大利润是多少元?
背景:一次小组合作探究课上,小明将两个正方形按如图所示的位置摆放(点 、 、 在同一条直线上),发现 且 .
小组讨论后,提出了下列三个问题,请你帮助解答:
(1)将正方形 绕点 按逆时针方向旋转(如图 ,还能得到 吗?若能,请给出证明;若不能,请说明理由;
(2)把背景中的正方形分别改成菱形 和菱形 ,将菱形 绕点 按顺时针方向旋转(如图 ,试问当 与 的大小满足怎样的关系时,背景中的结论 仍成立?请说明理由;
(3)把背景中的正方形分别改写成矩形 和矩形 ,且 , , ,将矩形 绕点 按顺时针方向旋转(如图 ,连接 , .小组发现:在旋转过程中, 的值是定值,请求出这个定值.






 圆锥
圆锥 圆柱
圆柱 三棱柱
三棱柱 正方体
正方体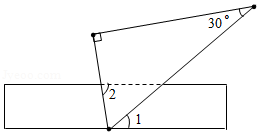




 粤公网安备 44130202000953号
粤公网安备 44130202000953号