江苏省扬州市江都区七校联谊九年级上学期期中数学试卷
关于x的一元二次方程 的根的情况是( )
的根的情况是( )
| A.有两个不相等的实数根 | B.可能有实数根,也可能没有 |
| C.有两个相等的实数根 | D.没有实数根 |
甲、乙、丙、丁四名射击运动员参加射击预选赛,他们射击成绩的平均环数 及方差
及方差 如下表所示.
如下表所示.
| |
甲 |
乙 |
丙 |
丁 |
 |
8 |
9 |
9 |
8 |
 |
1 |
1 |
1.2 |
1.3 |
若要选出一个成绩较好且状态稳定的运动员去参赛,那么应选运动员( )
A.甲 B.乙 C.丙 D.丁
如图,△ABC内接于⊙O,OD⊥BC于D,∠A=50°,则∠COD的度数是( )

| A.40° | B.45° | C.50° | D.60° |
股票每天的涨、跌幅均不超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停;当跌了原价的10%后,便不能再跌,叫做跌停。已知一支股票某天跌停,之后两天时间又涨回到原价,若这两天此股票股价的平均增长率为 ,则
,则 满足的方程是( )
满足的方程是( )
A. |
B. |
C. |
D. |
如图,已知直线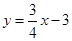 与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
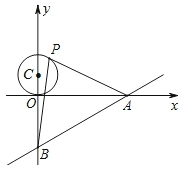
A.8 B.12 C.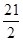 D.
D.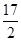
某班七个兴趣小组人数分别为4,4,5,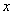 ,6,6,7. 已知这组数据的平均数是5,则这组数据的方差是 .
,6,6,7. 已知这组数据的平均数是5,则这组数据的方差是 .
13.若非零实数a、b、c满足 , 则关于x的一元二次方程
, 则关于x的一元二次方程 一定有一个根为____________.
一定有一个根为____________.
一块△ABC余料,已知AB=8cm,BC=15cm,AC=17cm,现将余料裁剪成一个圆形材料,则该圆的最大面积是 .
如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,点Q走过的路径长为 .

(本题8分) 已知:关于x的方程4x2 (k+2)x+k-3=0.
(k+2)x+k-3=0.
(1)求证:不论k取何值时,方程总有两个不相等实数根;
(2)试说明无论k取何值,方程都不存在有一根x=1的情况。
(本题10分)某学习小组想了解扬州市“迎建城2500周年”健身活动的开展情况,准备采用以下调查方式中的一种进行调查:①从一个社区随机选取200名居民;②从一个城镇的不同住宅楼中随机选取200名居民;③从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象.
(1)在上述调查方式中,你认为最合理的是 (填序号);
(2)由一种比较合理的调查方式所得到的数据制成了如图所示的频数分布直方图,请直接写出这200名居民健身时间的众数、中位数;
(3)小明在求这200名居民每人健身时间的平均数时,他是这样分析的:

小明的分析正确吗?如果不正确,请求出正确的平均数;
(4)若我市有800万人,估计我市每天锻炼2小时及以上的人数是多少?

(本题10分)如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长.
(本题10分)如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=2 .
.
(1)求证:AC是⊙O的切线;
(2)求由线段AC、AD与弧CD所围成的阴影部分的面积.(结果保留π)
(本题10分)如图13-1,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为 米.
米.
(1)用含 的式子表示花圃的面积;
的式子表示花圃的面积;
(2)如果通道所占面积是整个长方形空地面积的 ,求出此时通道的宽;
,求出此时通道的宽;
(3)若按上述要求施工,同时校长希望长方形花圃的形状与原长方形空地的形状相似,聪明的你想一想能不能满足校长的要求,若能,求出此时通道的宽;若不能,则说明理由。
(本题12分).如图1,在平面直角坐标系xoy中,M是x轴正半轴上一点,⊙M与x轴的正半轴交于A,B两点,A在B的左侧,且OA,OB的长是方程x2-12x+27=0的两根,ON是⊙M的切线,N为切点,N在第四象限.
(1)求⊙M的直径的长.
(2)如图2,将△ONM沿ON翻转180°至△ONG,求证△OMG是等边三角形.
(3)求直线ON的解析式.
 (a、b、c为常数)
(a、b、c为常数)


 ,则
,则 的值为( )
的值为( ) 的解为__________.
的解为__________. 的两个实数根,则矩形ABCD的周长为 .
的两个实数根,则矩形ABCD的周长为 .
 (用配方法解)
(用配方法解) ﹣
﹣ )÷
)÷ ,其中,a是方程x2+3x+1=0的根.
,其中,a是方程x2+3x+1=0的根.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号