江苏省无锡市锡北片七年级下学期期中考试数学试卷
有两根13cm,15cm的木棒,要想以这两根木棒做一个三角形,可以选用第三根木棒的长为( )
| A.2cm | B.11cm | C.28cm | D.30cm |
如图,在 方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个长方形,那么,下面的平移方法中,正确的是( )
方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个长方形,那么,下面的平移方法中,正确的是( )
| A.先向下平移3格,再向右平移1格 |
| B.先向下平移2格,再向右平移1格 |
| C.先向下平移2格,再向右平移2格 |
| D.先向下平移3格,再向右平移2格 |
如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AD∥BE,且∠D=∠B;其中,能推出AB∥DC的条件为( )
| A.①② | B.①③ | C.②③ | D.以上都错 |
已知a,b,c是三角形的三边,那么代数式 的值( )
的值( )
| A.大于零 | B.小于零 | C.等于零 | D.不能确定 |
已知 ,则下列结论正确的是( )
,则下列结论正确的是( )
| A.2m-n=1 | B.2m-n=3 | C.2m+n=3 | D.2m=3n |
连结多边形不相邻的两个顶点的线段,叫做多边形的对角线.观察上述图形并阅读相关文字,思考回答问题:显然四边形对角线有2条;五边形的对角线有5条;对于六边形的对角线条数,光靠“数”数,也能数出来,但已感到较麻烦!需寻找规律!从一个顶点A出发,显然有3条,同理从B出发也3条,每个顶点出发都是3条,但从C顶点出发,就有重复线段!用此方法算出六边形的对角线条数为a;且能归纳出n边形的对角线条数的计算方法;若一个n边形有35条对角线,则a和n的值分别为( )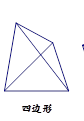

| A.12,20 | B.12,15 | C.9,10 | D.9,12 |
如图,将周长为10的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为 .
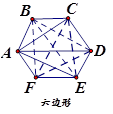
△ABC中,∠ABC=40°,∠ACB=80°,BO、CO分别平分∠ABC,∠ACB,交于O,CI为外角∠ACD的平分线,BO的延长线交CI于I点,记∠BAC=∠1,∠BIC=∠2,则∠1:∠2= (求比值).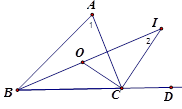
如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.
(1)若∠B=35°,∠ACB=85°,则∠E的度数= ;
(2)当P点在线段AD上运动时,设∠B=α,∠ACB=β(β>α),则∠E= .(用α,β的代数式表示)
计算(前3题,每题3分,第4题5分,共14分)
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;(本题先化简,再求值,其中
;(本题先化简,再求值,其中 )
)
画图并填空:
如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点C的对应点C′.
(1)画出平移后的△A′B′C′,(利用网格点和三角板画图)
(2)画出AB边上的高线CD;
(3)画出BC边上的中线AE;
(4)在平移过程中高CD扫过的面积为 .(网格中,每一小格单位长度为1)
如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.请将解题过程填写完整.(填理由或相应内容)
解:∵EF∥AD(已知)∴∠2=①(② ),
又∵∠1=∠2(已知)∴∠1=∠3(等量代换),
∴AB∥③ ,∴∠BAC+ ④ =180°(⑤ )
∵∠BAC=70°(已知),∴∠AGD=⑥ .
请同学们把上述①②③ ④上的内容,填在答卷横线上!
如图,有足够多的边长为a的小正方形(A类)、长为a,宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2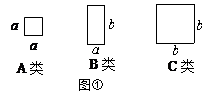
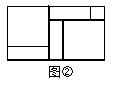
 图③
图③
(1)若取其中的若干个(三种图形都要取到)拼成一个长方形,使其面积为3a2+5ab+2b2,在虚框中画出图形,并根据所画图形,将多项式3a2+5ab+2b2分解因式为 .
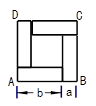
(2)如图③,是用B类长方形(4个)拼成的图形,其中四边形ABCD是大正方形,边长为m,里面是一个空洞,形状为小正方形,边长为n,观察图案并判断,将正确关系式的序号填写在横线上_____________(填写序号)①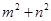 = 2(a2+b2 ); ②
= 2(a2+b2 ); ②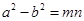 ; ③
; ③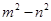 = 4ab
= 4ab
先阅读下面的内容,再解决问题,
例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
解:∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0,n﹣3=0
∴m=﹣3,n=3
(1)若x2+2y2﹣2xy+4y+4=0,求xy的值.
(2)已知整数a、b、c是不等边△ABC的三边长,满足a2+b2=6a+8b﹣25,且c是△ABC中最长的边,求c的值.
观察下表多项式分解因式的特征,并回答问题.
| 1 |
2 |
3 |
4 |
| 多项式 |
常数项 |
一次项系数 |
分解因式 |
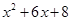 |
8=2×4 |
6=2+4 |
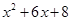 =(x+2)(x+4) =(x+2)(x+4) |
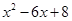 |
8=(-2)×(-4) |
-6=(-2)+(-4) |
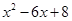 =(x-2)(x-4) =(x-2)(x-4) |
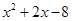 |
-8=4×(-2) |
2=4+(-2) |
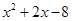 =(x+4)(x-2) =(x+4)(x-2) |
对于二次项系数为1的二次三项式,若符合上述表中(2)(3)栏目的特征,就可以采用表中方法进行因式分解.
(1)分解因式: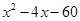 ;
;
(2)若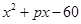 可分解为两个一次因式的积,则整数p的值有 个;
可分解为两个一次因式的积,则整数p的值有 个;








 提出一个公因式
提出一个公因式 后,另一个因式是 .
后,另一个因式是 . 是一个完全平方式,那么负数m的值为 .
是一个完全平方式,那么负数m的值为 .
 ,
, ,则
,则 =_____;
=_____; = ;
= ; ;
; ;
; ;
;

 粤公网安备 44130202000953号
粤公网安备 44130202000953号