江苏省泰州市九年级中考二模数学试卷
甲、乙两名同学在一次用频率去估计概率的实验中,绘出了某一结果出现的频率的折线图,则符合这一结果的实验可能是
| A.掷一枚正六面体的骰子,出现1点的概率 |
| B.抛一枚硬币,出现正面的概率 |
| C.任意写一个整数,它能被2整除的概率 |
| D.从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率 |
如图, ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=
ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG= cm,则EF的长为
cm,则EF的长为
| A.2cm | B. cm cm |
C.1cm | D. cm cm |
十八大开幕当天,网站关于某一信息的总浏览量达550000000次.将550000000用科学记数法表示为 .
某排球队12名队员的年龄如下表所示:
| 年龄/岁 |
19 |
20 |
21 |
22 |
23 |
| 人数/人 |
1 |
5 |
3 |
1 |
2 |
则该队队员年龄的中位数是 .
如图,点A、B在直线MN上,AB=8cm,⊙A、⊙B的半径均为1cm.⊙A以每秒1cm的速度自左向右运动;与此同时,⊙A的半径也随之增大,其半径r(cm)与时间t(秒)之间满足关系式r=1+t(t≥0).则当点A出发后 秒,两圆相切.
如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y= (k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,
(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,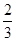 ),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是
),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是 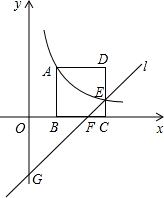
如图,在△ABC和△ACD中,CB=CD,设点E是CB的中点,点F是CD的中点.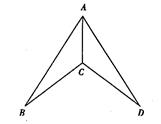
(1)请你在图中作出点E和点F(要求用尺规作图,保留作图痕迹,不写作法与证明);
(2)连接AE、AF,若∠ACB=∠ACD,则△ACE与△ACF全等吗?请说明理由.
某校实施课堂教学改革后,学生的自主学习、合作交流能力有了很大提高.九(2)班的陈老师为了解本班学生自主学习、合作交流的具体情况,对部分同学进行了一段时间的跟踪调查,将调查结果(分为A:特别好;B:好;C:一般;D:较差四类)绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题: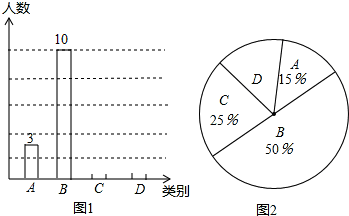
(1)本次调查中,陈老师一共调查了 名同学,并补全条形统计图;
(2)扇形统计图中,D类所占圆心角为 度;
(3)为了共同进步,陈老师想从被调查的A类(1名男生2名女生)和D类(男女生各占一半)中分别选取一位同学进行“一帮一”互助学习,请用画树形图或列表的方法求所选的两位同学恰好是一男一女的概率.
某中学九年级一位同学不幸得了重病,牵动了全校师生的心,该校开展了“献爱心”捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.
(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;
(2)按照(1)中收到捐款的增长速度,第四天该校能收到多少捐款?
“五一”假期间,小华到小明家邀请小明到新华书店看书,当小华到达CD(点D是小华的眼睛)处时,发现小明在七楼 处,此时测得仰角为45°,继续向前走了10m到达
处,此时测得仰角为45°,继续向前走了10m到达 处,发现小明在六楼B处,此时测得仰角为
处,发现小明在六楼B处,此时测得仰角为 ,已知楼层高AB=3m,求O
,已知楼层高AB=3m,求O 的长. (结果保留根号)
的长. (结果保留根号)
如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点.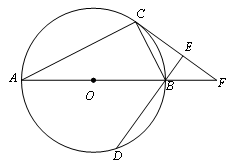
(1)求证:CF为⊙O的切线;
(2)若⊙O的半径为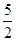 cm,弦BD的长为3 cm,求CF的长.
cm,弦BD的长为3 cm,求CF的长.
实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=–200x2+400x表示;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y= (k>0)表示(如图所示).
(k>0)表示(如图所示).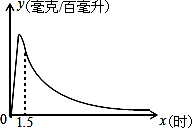
(1)喝酒后多长时间血液中的酒精含量达到最大值?最大值为多少?
(2)当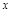 =5时,y=45.求k的值.
=5时,y=45.求k的值.
(3)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
如图,矩形ABCD中,P是边AD上的一动点,连接BP、CP,过点B作射线交线段CP的延长线于点E,交AD边于点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x,PM=y.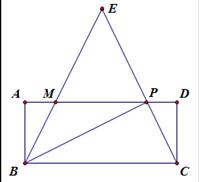
(1)说明△ABM∽△APB;并求出y关于x的函数关系式,写出自变量x的取值范围;
(2)当AP=4时,求sin∠EBP的值;
(3)如果△EBC是以∠EBC为底角的等腰三角形,求AP的长。





 在实数范围内有意义,则x的取值范围是
在实数范围内有意义,则x的取值范围是

 的图象不经过
的图象不经过
 ,那么x2– y2= .
,那么x2– y2= .
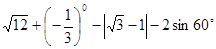
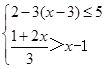 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.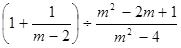 ,其中m = 4.
,其中m = 4.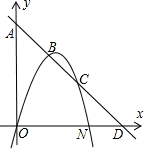
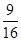 ?若存在,求出动点P的位置;若不存在,请说出理由.
?若存在,求出动点P的位置;若不存在,请说出理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号