四川省丹棱县九年级第一次诊断性考试数学试卷
正在建设的成都第二绕城高速全长超过220公里,串起成都市二、三圈层及周边的广汉、简阳等地,总投资达到290亿元.用科学记数法表示290亿元应为( )
A. 元 元 |
B. 元 元 |
C. 元 元 |
D. 元 元 |
如图,是由几个小立方块所搭成的几何体的俯视图,小正方体中的数字表示在该位置上的小立方块的个数,这个几何体的主视图是( ) 
如图,把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为( )
| A.125° | B.120° | C.140° | D.130° |
如图,扇形折扇完全打开后,如果张开的角度(∠BAC)为120°,骨柄AB的长为 ,扇面的宽度BD的长为
,扇面的宽度BD的长为 ,那么这把折扇的扇面面积为( )
,那么这把折扇的扇面面积为( )
A. B.
B. C.
C. D.
D.
下列命题中,真命题是( )
| A.对角线相等的四边形是矩形 |
| B.对角线互相垂直平分的四边形是菱形 |
| C.一组对边平行,另一组对边相等的四边形是平行四边形 |
| D.一组邻边相等,并且有一个内角为直角的四边形是正方形 |
如图,已知圆柱底面的周长为4dm,圆柱高为2dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为( )
A. dm dm |
B. dm dm |
C. dm dm |
D. dm dm |
有3张边长为 的正方形纸片,4张边长分别为
的正方形纸片,4张边长分别为 、
、 (
( )的长方形纸片,5张边长为
)的长方形纸片,5张边长为 的正方形纸片,从其中抽取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(按原纸张进行无空隙、无重叠拼接),则拼成的正方形的边长最长可以为( )
的正方形纸片,从其中抽取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(按原纸张进行无空隙、无重叠拼接),则拼成的正方形的边长最长可以为( )
A. |
B. |
C. |
D. |
如图,在平面直角坐标系中,的圆心坐标是(3, )(
)( ),半径为3,函数
),半径为3,函数 的图象被截得的弦AB的长为
的图象被截得的弦AB的长为 ,则
,则 的值是( )
的值是( )
| A.4 | B. |
C. |
D. |
如图所示,在△ABC中,BC=8,E、F分别是AB、AC的中点,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于点Q,当 时,
时, .
.
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.
(1)点A的坐标为 ,点C的坐标为 .
(2)将△ABC向左平移7个单位,请画出平移后的 ,若M为△ABC内的一点,其坐标为(
,若M为△ABC内的一点,其坐标为( ,
, )则平移后点
)则平移后点 的坐标为 .
的坐标为 .
(3)以原点O为位似中心,将△ABC缩小,使变换后的 与△ABC对应边的比为1:2,请在网格内画出一个
与△ABC对应边的比为1:2,请在网格内画出一个 ,则
,则 的坐标为 .
的坐标为 .
钓鱼岛自古以来就是中国的领土.如图,我国甲、乙两艘海监执法船某天在钓鱼岛附近海域巡航,某一时刻这两艘船分别位于钓鱼岛正西方向的A处和正东方向的B处,这时两船同时接到立即赶往C处海域巡查的任务,并测得C处位于A处北偏东59°方向、位于B处北偏西44°方向.若甲、乙两船分别沿AC,BC方向航行,其平均速度分别是20海里/小时,18海里/小时,试估算哪艘船先赶到C处.
(参考数据:cos59°≈0.52,sin46°≈0.72)
一个不透明的口袋里装有分别标有汉字“大”、“雅”、“丹”、“棱”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“丹”的概率为多少?
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图的方法,求出甲取出的两个球上的汉字恰能组成“大雅”或“丹棱”的概率 ;
;
(3)乙从中任取一球,记下汉字后再放回袋中,然后再从中任取一球,记下汉字,则乙取出的两个球上的汉字恰能组成“大雅”或“丹棱”的概率为 ,请指出
,请指出 ,
, 的大小关系.
的大小关系.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙边(两边足够长),用 长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),设
长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),设 .
.
(1)若花园的面积为 ,求
,求 的值;
的值;
(2)若在 处有一棵树与墙CD、AD的距离分别是
处有一棵树与墙CD、AD的距离分别是 和
和 ,要将这棵树围在花园内(含边界、不考虑树的粗细),求花园面积
,要将这棵树围在花园内(含边界、不考虑树的粗细),求花园面积 的最大值.
的最大值.
在菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.
(1)比较∠F和∠ABD的大小,并说明理由;
(2)当△BFC有一个内角是直角时,求证:△BFC∽△EFA;
(3)当△BFC与△EFA相似(两三角形的公共角为对应角),且AC=12,DE=5时,求△BFC与△EFA的相似比.

 等于( )
等于( )



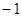 ,
, ),B(2,
),B(2, ),C(3,
),C(3, )都在反比例函数
)都在反比例函数 的图象上,那么( )
的图象上,那么( )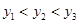



 的一元二次方程
的一元二次方程 的两个不相等的实数根
的两个不相等的实数根 、
、 满足
满足 ,那么
,那么 的值为( )
的值为( )



 .
.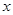 ,4,5.若这组数据的中位数是3,则这组数据的方差是 .
,4,5.若这组数据的中位数是3,则这组数据的方差是 . 中,如果
中,如果 ,
, 满足
满足 ,那么
,那么 .
. 的分式方程
的分式方程 有增根,则
有增根,则 = .
= . 的部分图象如图所示,则关于
的部分图象如图所示,则关于 的一元二次方程
的一元二次方程 的解为 .
的解为 .

 ,其中
,其中 ,
, .
. 与
与 轴交于点C,与
轴交于点C,与 轴交于点A(
轴交于点A( ,0),B(
,0),B( ,0).
,0).
 与抛物线交于点Q、C两点,过点D作直线DF⊥
与抛物线交于点Q、C两点,过点D作直线DF⊥ ?若存在,请求出点D的坐标;若不存在,请说明理由.
?若存在,请求出点D的坐标;若不存在,请说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号