浙江省东阳七校八年级上学期期中考试数学试卷
下列语句是命题的是( )
| A.作线段AB的中点 |
| B.作线段AB的垂直平分线 |
| C.等角的补角相等吗? |
| D.对顶角不相等 |
两根木棒的长分别是5cm和7cm,要选择第三根木棒,将他们首尾相接钉成一个三角形。则第三根木棒长的取值可以是( )
| A.2 cm | B.4 cm | C.12 cm | D.13 cm |
以下是回收、绿色包装、节水、低碳四个标志,其中是轴对称图形的是( )
A. |
B. |
C. |
D. |
若等腰三角形的两边长分别是2和6,则这个三角形的周长是 ( )
| A.14 | B.10 | C.14或10 | D.以上都不对 |
在平面直角坐标系中,点P(2,3)关于y轴的对称点在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
等腰三角形一腰上的高与另一腰的夹角为40°,则其顶角为( )
| A.50° | B.130° | C.50°或130° | D.55°或130° |
下列命题:①内错角相等;②面积相等的两个三角形全等;③钝角三角形的三条高线所在直线的交点在三角形内; ④等腰三角形两底角的平分线相等。其中真命题是( )
| A.① | B.② | C.③ | D.④ |
如图所示,△ABC是在2×2的正方形网格中以格点为顶点的三角形,那么图中与△ABC成轴对称且也以格点为顶点的三角形共有( )
| A.3个 | B.4个 | C.5个 | D.6个 |
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ。以下五个结论:
①AD=BE;
②PQ∥AE;
③AP=BQ;
④DE=DP;
⑤∠AOB=60°
成立的结论个数是( )
| A.2 | B.3 | C.4 | D.5 |
将以点(1,6),(-2,6)为端点的线段向下平移8个单位长度,则所得的像上的任意一点的坐标是 。
已知ΔABC中 AB=13cm, AC="20cm" ,第三边BC边上的高AD=12cm,则BC的长为_____cm。
如图,一个粒子在第一象限内及x轴,y轴上运动,第一分钟内从原点运动到(1,0),第二分钟从(1,0)运动到(1,1),而后它接着按图中箭头所示的与x轴,y轴平行的方向来回运动,且每分钟移动1个长度单位。
(1)当粒子所在位置是(2,2)时,所经过的时间是 ;
(2)在第2014分钟时,这个粒子所在位置的坐标是 。
解不等式(组)并把不等式组的解集在数轴上表示出来:
(1)7x-2≥5x+2 ;
(2)
尺规作图:已知:∠α,线段a, b 求作:△ABC,使∠A= , AB="a," AC=b。
, AB="a," AC=b。
( 不写作法,保留痕迹,写出结论 )
如图, 已知:AC⊥BC于点C, AD⊥BD于点D,点E是AB中点,若CD=7, AB=12,求△CDE的周长。
如图,等边三角形ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M,则M是BE的中点,请说明理由。
实验中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。
(1)购买一个足球、一个篮球各需多少元?
(2)根据实验中学的实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不低于5600但不超过5720元,可以有哪几种购买方案?
(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E。
证明:DE=BD+CE。
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由。
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状,并给出证明。
 的整数解共有5个,则a的取值范围为_________。
的整数解共有5个,则a的取值范围为_________。 =60°,
=60°,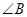 =30°,
=30°,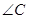 =20°,求
=20°,求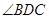 的度数。
的度数。

 粤公网安备 44130202000953号
粤公网安备 44130202000953号