河南省三门峡市九年级上学期期末考试数学试卷
如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,分别以A、C为圆心,以 的长为半径作圆,将Rt△ABC截去两个扇形,则剩余(阴影)部分的面积为 .
的长为半径作圆,将Rt△ABC截去两个扇形,则剩余(阴影)部分的面积为 .
已知一元二次方程2x2+mx-7=0的一个根为x=1则另一根为( )
| A.1 | B.2 | C.-3.5 | D.-5 |
下列事件是必然事件的是( )
| A.某运动员射击一次击中靶心 |
| B.抛一枚硬币,正面朝上 |
| C.3个人分成两组,一定有2个人分在一组 |
| D.明天一定晴天 |
等边三角形旋转一定角度后能与自身重合,则旋转的角度可能是( )
| A.30° | B.60° | C.90° | D.120° |
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数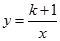 的图象上.若点A的坐标为(-2,-2),则k的值为( )
的图象上.若点A的坐标为(-2,-2),则k的值为( )
| A.3 | B.4 | C.-4 | D.-5 |
如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=15°,∠AOB′的度数是( )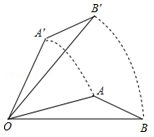
| A.25° | B.30° | C.35° | D.40° |
如图,⊙O中,四边形ABDC是圆内接四边形,若∠BOC=110°,则∠BDC的度数是 ( )
| A.110° | B.70° | C.55° | D.125° |
抛物线 可以由抛物线y=x2平移得到,则下列平移过正确的是( )
可以由抛物线y=x2平移得到,则下列平移过正确的是( )
| A.先向左平移2个单位,再向上平移3个单位 |
| B.先向左平移2个单位,再向下平移3个单位 |
| C.先向右平移2个单位,再向下平移3个单位 |
| D.先向右平移2个单位,再向上平移3个单位 |
三角形两边长分别是8和6,第三边长是一元二次方程 一个实数根,则该三角形的面积是( )
一个实数根,则该三角形的面积是( )
| A.24 | B.48 | C.24或 |
D. |
如图,已知点A、B、C的坐标分别为(0,0),(4,0),(5, 2)将△ABC绕点A按逆时针方向旋转90°得到△AB′C′.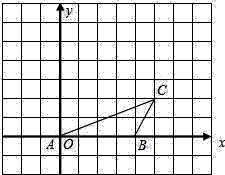
(1)画出△AB′C′;
(2)求点C′的坐标
2015年元旦,某商场开展购物抽奖活动,抽奖箱中有4个标号分别为1,2,3,4的质地、大小相同的小球,顾客任意摸取一个小球,然后放回,再摸取一个小球,若两次摸出的数字之和为“8”获一等奖,数字之和为“6”获二等奖,数字之和为其他数字则获三等奖,请用列举法分别求出顾客抽中一、二、三等奖的概率.
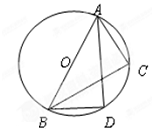
如图,⊙O经过菱形ABCD的三个顶点A、C、D,且与AB相切于点A
(1)求证:BC为⊙O的切线;
(2)求∠B的度数.
如图,直线 与反比例函数
与反比例函数 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为( ,m).
,m).
(1)求反比例函数的解析式;
(2)若点P(n,-1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.
如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式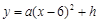 ,已知球网与O点的水平距离为9m,球网高度为2.43m,球场另一边的底线距O点的水平距离为18m.
,已知球网与O点的水平距离为9m,球网高度为2.43m,球场另一边的底线距O点的水平距离为18m.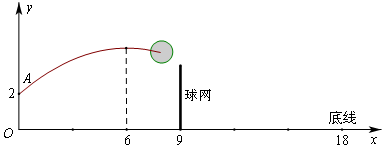
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出底线?请说明理由;
(3)若球一定能越过球网,且刚好落在底线上,求h的值.
 的解为 .
的解为 .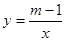 的图象如图所示,则实数m的取值范围是 .
的图象如图所示,则实数m的取值范围是 .
 与反比例函数
与反比例函数 相交于点E(
相交于点E( ,2),若
,2),若 ,则
,则 的取值范围为 .
的取值范围为 .
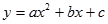 的图象的一部分,请你根据图象写出方程
的图象的一部分,请你根据图象写出方程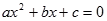 的两根是 .
的两根是 .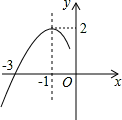
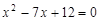 的两根,则这两个圆的位置关系是 .
的两根,则这两个圆的位置关系是 .

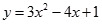 与轴
与轴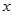 的交点的个数为 ( )
的交点的个数为 ( )
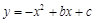 过(1,4)与(4,-5)两点,且.与一直线
过(1,4)与(4,-5)两点,且.与一直线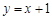 相交于A,C两点
相交于A,C两点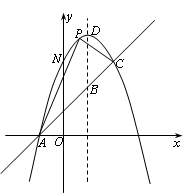
 粤公网安备 44130202000953号
粤公网安备 44130202000953号