江苏省阜宁县九年级上学期期末考试数学试卷
县医院住院部在连续10天测量某病人的体温与36℃的上下波动数据为:0.2, 0.3, 0.1, 0.1, 0, 0.2, 0.1, 0.1, 0.1, 0,则对这10天中该病人的体温波动数据分析不正确的是
| A.平均数为0.12 | B.众数为0.1 | C.中位数为0.1 | D.方差为0.02 |
△ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是
| A.80° | B.160° | C.100° | D.80°或100° |
若二次函数 的
的 与
与 的部分对应值如下表:
的部分对应值如下表:
 |
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
| y |
-27 |
-13 |
-3 |
3 |
5 |
3 |
则当 时,
时, 的值为
的值为
A.5 B.-3 C.-13 D.-27
如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、 C两点,已知B(8,0),C(0,6),则⊙A的半径为
A.3 B.4 C.5 D.8
如图,在△ABC中,EF∥BC, ,S四边形BCFE=8,则S△ABC等于
,S四边形BCFE=8,则S△ABC等于
| A.9 | B.10 | C.12 | D.13 |
二次函数 的图象如图所示,反比例函数
的图象如图所示,反比例函数 与正比例函数
与正比例函数 在同一坐标系中的大致图象可能是
在同一坐标系中的大致图象可能是
A. B. C. D.
不透明的袋子中装有4个红球、3个黄球和5个蓝球,每个球除颜色不同外其它都相同,从中任意摸出一个球,则摸出 球的可能性最大.
已知一组数据x1,x2,x3,x4,x 5的方差是 ,那么另一组数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的方差是 .
,那么另一组数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的方差是 .
如图,在相距2米的两棵树间拴一根绳子做一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小芳距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为 米.
九年级某班同学在庆祝2015年元旦晚会上进行抽奖活动.在一个不透明的口
袋中有三个完全相同的小球,把它们分别标号1、2、3.随机摸出一个小球记下标号后放回摇匀,再从中随
机摸出一个小球记下标号.
(1)、请用列表或画树形图的方法(只选其中一种),表示两次摸出小球上的标号的所有结果;
(2)、规定当两次摸出的小球标号相同时中奖,求中奖的概率.
从全校1200名学生中随机选取一部分学生进行调查,调查情况:
| A.上网时 间  小时; 小时; |
B.1小时<上网时间 小时; 小时; |
C.4小时<上网时间 小时; 小时; |
D.上网时间>7小时.统计 |
结果制成了如图统计图:
(1)、参加调查的学生有 人;
(2)、请将条形统计图补全;
(3)、请估计全校上网不超过7小时的学生人数.
已知抛物线

(1)、该抛物线的对称轴是 ,顶点坐标 ;
(2)、选取适当的数据填入下表,并在直角坐标系内描点画出该抛物线的图象;
| x |
… |
|
|
|
|
|
… |
| y |
… |
|
|
|
|
|
… |
(3)、若该抛物线上两点A(x1,y1),B(x2,y2)的横坐标满足x1>x2>1,试比较y1与y2的大小.
某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为3万元,可变成本逐年增长,已知该养殖户第1年的可变成本为2.4万元,设可变成本平均每年增长的百分率为x.
(1)、用含x的代数式表示第3年的可变成本为 万元.
(2)、如果该养殖户第3年的养殖成本为6.456万元,求可变成本平均每年增长的百分率?
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)、求证:△ADF∽△DEC
(2)、若AB=4,AD=3 ,AE=3,求AF的长.
,AE=3,求AF的长.
已知二次函数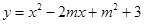 (
(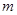 是常数).
是常数).
(1)、求证:不论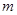 为何值,该函数的图象与x轴没有公共点;
为何值,该函数的图象与x轴没有公共点;
(2)、把该函数的图象沿 轴向下平移多少个单位长度后,得到的函数的图象与
轴向下平移多少个单位长度后,得到的函数的图象与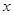 轴只有一个公共点?
轴只有一个公共点?
如图,某大楼的顶部树有一块广告牌CD,小明在山坡的坡脚A处测得广告牌
底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度 ,AB=10米,AE=15米.
,AB=10米,AE=15米.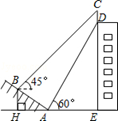
(1)、求点B距水平面AE的高度BH;
(2)、求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据: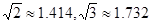 )
)
在一场2015亚洲杯赛B组第二轮比赛中,中国队凭借吴曦和孙可在下半场
的两个进球,提前一轮小组出线。如图,足球场上守门员在 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的 处飞出
处飞出
( 在
在 轴上),运动员孙可在距
轴上),运动员孙可在距 点6米的
点6米的 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点 ,距地面约4米
,距地面约4米
高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高
度减少到原来最大高度的一半.
(1)、求足球开始飞出到第一次落地时,该抛物线的函数表达式.
(2)、足球第一次落地点 距守门员多少米?(取
距守门员多少米?(取 )
)
(3)、孙可要抢到足球第二个落地点 ,他应从第一次落地点
,他应从第一次落地点 再向前跑多少米?(取
再向前跑多少米?(取 )
)
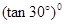 的值是
的值是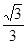
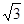
 的解是
的解是

 ,则AD=______。
,则AD=______。
 轴上,则k= .
轴上,则k= . ,则这个圆锥的高为 .
,则这个圆锥的高为 . (2)解方程:
(2)解方程:

 ,求⊙O的半径。
,求⊙O的半径。 粤公网安备 44130202000953号
粤公网安备 44130202000953号