同步九年级数学下册人教26.2实际问题与反比例函数
已知一块蓄电池的电压为定值,以此蓄电池为电源时,电流I(A)与电阻R(Ω)之间的函数关系如图,如果以此蓄电池为电源的用电器限制电流不超过10A,那么此用电器的可变电阻为( )
A.不小于3.2Ω B.不大于3.2Ω
C.不小于12Ω D.不大于12Ω
物理学知识告诉我们,一个物体所受到的压强p与所受压力F及受力面积S之间的计算公式为 .当一个物体所受压力为定值时,那么该物体所受压强p与受力面积S之间的关系用图象表示大致为( )
.当一个物体所受压力为定值时,那么该物体所受压强p与受力面积S之间的关系用图象表示大致为( )
A. |
B. |
C. |
D. |
某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图表示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I的函数解析式为( )
A. B.
B.
C. D.
D.
某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气球体积V的反比例函数,其图象如图所示,当气球内的气压大于120kPa时,气球将爆炸,为了安全,气球的体积应该( )
A.不大于 m3 m3 |
B.小于 m3 m3 |
C.不小于 m3 m3 |
D.小于 m3 m3 |
一张正方形的纸片,剪去两个一样的小矩形得到一个“E”形图案,如图所示,设小矩形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是( )
A. |
B. |
C. |
D. |
已知两点P1(x1,y1),P2(x2,y2)在函数 的图象上,当x1>x2>0时,下列结论正确的是( )
的图象上,当x1>x2>0时,下列结论正确的是( )
| A.0<y1<y2 | B.0<y2<y1 |
| C.y1<y2<0 | D.y2<y1<0 |
如图,已知一次函数y=ax+b的图象和反比例函数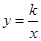 的图象相交于A,B两点,则不等式
的图象相交于A,B两点,则不等式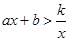 的解集为( )
的解集为( )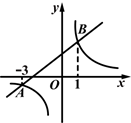
| A.x<-3 | B.-3<x<0或x>1 |
| C.x<-3或x>1 | D.-3<x<1 |
设从泉州到福州乘坐汽车所需的时间是t(小时),汽车的平均速度为v(千米/时),则下面大致能反映v与t的函数关系的图象是( )
A. |
B. |
C. |
D. |
一块砖所受的重力为14.7N,它的长、宽、高分别为20cm、10cm、5cm,将砖平放时对地面的压强是( )
| A.735Pa | B.753Pa | C.73.5Pa | D.75.3Pa |
如图,一次函数y1=k1x+b(k1,b为常数,且k1≠0)的图象与反比例函数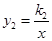 (k2为常数,且k2≠0)的图象都经过点A(2,3),则当x>2时,y1与y2的大小关系为( )
(k2为常数,且k2≠0)的图象都经过点A(2,3),则当x>2时,y1与y2的大小关系为( )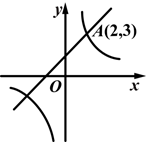
| A.y1>y2 | B.y1=y2 |
| C.y1<y2 | D.以上说法都不对 |
某体育场计划修建一个容积一定的长方体游泳池,设容积为a(m3),泳池的底面积S(m2)与其深度x(m)之间的函数关系式为 (x>0),该函数的图象大致是( )
(x>0),该函数的图象大致是( )
A. |
B. |
C. |
D. |
在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也随之改变.密度ρ(单位:kg/m3)与体积V(单位:m3)满足函数解析式 (k为常数,k≠0),其图象如图所示,则k的值为( )
(k为常数,k≠0),其图象如图所示,则k的值为( )
| A.9 | B.-9 |
| C.4 | D.-4 |
如图,OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线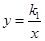 和
和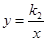 的一个分支上,分别过点A、C作x轴的垂线,垂足分别为M、N,有以下的结论:
的一个分支上,分别过点A、C作x轴的垂线,垂足分别为M、N,有以下的结论:
①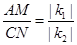 ;
;
②阴影部分的面积是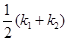 ;
;
③当∠AOC=90°时,|k1|=|k2|;
④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.
其中正确的结论是________(把所有正确结论的序号都填上).
某工作人员打算利用不锈钢条制作一个面积为0.8m2的矩形模具.设矩形模具的长为ym,宽为xm.
(1)写出y与x之间的函数关系式,并说明y与x之间是什么函数关系;
(2)若使模具长比宽多1.6m.已知每米这种不锈钢条的价格为6元,制作这个模具共需花多少钱?
在研究气体压强和体积关系的物理实验中,一个气球内充满了一定质量的气体,实验中气体温度保持不变,实验人员记录了实验过程中气球内的气体压强p(kPa)与气体体积V(m3)的数据如下表:
| V(m3) |
0.8 |
1.2 |
1.6 |
2.0 |
2.4 |
| p(kPa) |
120 |
80 |
60 |
48 |
40 |
(1)根据表中的数据判断p是V的________.(①一次函数;②反比例函数;③二次函数.填序号即可)
(2)确定p与V的函数关系式,并在如图所示的坐标系内画出该函数的大致图象;
(3)当气球内的气体压强大于140kPa时,气球将爆炸,为了安全起见,气体的体积V(m3)的取值范围是________.
工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料煅烧到800℃,然后停止煅烧进行锻造操作.经过8min时,材料温度降为600℃.煅烧时,温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图),已知该材料初始温度是32℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作,那么锻造的操作时间有多长?
为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后,y与x成反比例(如图).现测得药物8分钟燃烧完毕,此时室内空气中每立方米的含药量为6毫克.请根据题中提供的信息,解答下列问题:
(1)药物燃烧时和药物燃烧后,分别求出y关于x的函数表达式及自变量x的取值范围;
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时,学生方可进教室,那么从消毒开始,至少需要经过多少分钟,学生才能回到教室?
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
 的图象在同一平面角坐标系中大致是( )
的图象在同一平面角坐标系中大致是( )



 经过点(-2,1),则k的值为________.
经过点(-2,1),则k的值为________. 的图象上的一点,MA垂直于y轴,垂足为A,△MAO的面积为2,则k的值为________.
的图象上的一点,MA垂直于y轴,垂足为A,△MAO的面积为2,则k的值为________.
 (k≠0)的图象上,则k的值为________.
(k≠0)的图象上,则k的值为________. 在第一象限内的图象交于点C,且A为BC的中点,则k=________.
在第一象限内的图象交于点C,且A为BC的中点,则k=________.
 (k是为常数,k≠0)的图象位于第一、第三象限,写出一个符合条件的k值为________.
(k是为常数,k≠0)的图象位于第一、第三象限,写出一个符合条件的k值为________. ,则这个反比例函数的表达式为________.
,则这个反比例函数的表达式为________. 粤公网安备 44130202000953号
粤公网安备 44130202000953号