江苏省盐城市盐都区西片八年级12月月考数学试卷
点A(-2, -3)在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
在实数 , -
, - ,-3.14,0,
,-3.14,0, 中,无理数有 ( )
中,无理数有 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |
下列函数关系式:①y=-x;②y=2x+11;③y=x2+x+1 ④y= .其中一次函数的个数是
.其中一次函数的个数是
| A.1个 | B.2个 | C.3个 | D.4个 |
到三角形三个顶点的距离相等的点一定是( )
| A.三条高的交点 |
| B.三条中线的交点 |
| C.三条垂直平分线的交点 |
| D.三条角平分线的交点 |
下列条件中,不能判定两个三角形全等的是( )
| A.两边一角对应相等 |
| B.两角一边对应相等 |
| C.三边对应相等 |
| D.直角边和一个锐角对应相等 |
2014年6月3日中央新闻报道,为鼓励居民节约用水,北京市将出台新的居民用水收费标准:若每月每户居民用水不超过4m3,则按每立方米2元计算;若每月每户居民用水超过4m3,则超过部分按每立方米4.5元计算(不超过部分仍按每立方米2元计算)。现假设该市某户居民用水x m3,水费为y元,则y与x的函数关系式用图象表示正确的是
目前我国总人口数约为133900000,用科学计数法可表示为 (精确到1000000)
已知点A(-4,a),B(-2,b)都在直线 (k为常数)上,则a与b的大小关系是a________b(填“<”“=”或“>”=);
(k为常数)上,则a与b的大小关系是a________b(填“<”“=”或“>”=);
已知直线y=kx+b与y=2x+1平行,且经过点(-3,4),则k=____,b=_____;
如图,直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式kx+b<4x+2的解集为 。
已知无论n取什么实数,点P(n, 4n-3)都在直线l上,若Q(a, b)是直线l上的点,则(4a-b)2的值等于 。
有两棵树,一棵高7米,另一棵高2米,两树相距12米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,请问小鸟至少飞行多少米.
如图, 已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连结QE并延长交BP于点F.
(1)试说明:∠AEQ=90°;
(2)猜想EF与图中哪条线段相等(不能添加辅助线产生新的线段),并说明理由.
某医药研究所开发了一种新药,在试验时发现,如果成人按规定剂量服用2小时时血液中含药量最高,达每毫升6微克,接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随服药后时间x(小时)的变化如图所示,当成人按规定剂量服药后。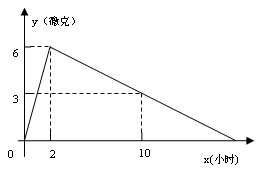
⑴分别求出x<2与x>2时y与x的函数关系式
⑵如果每毫升血液中含药量为或3微克以上时,在治疗时是有效的,那么这个有效时间是多长?
甲、乙两车分别从相距200千米的A、B两地同时出发相向而行,甲到B地后立即返回,乙到A地后停止行驶,下图是它们离各自出发地的距离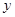 (km)与行驶时间
(km)与行驶时间 (h)之间的函数图象.
(h)之间的函数图象.
(1)请直接写出甲离出发地A的距离 (km)与行驶时间
(km)与行驶时间 (h)之间的函数关系式,并写出自变量
(h)之间的函数关系式,并写出自变量 的取值范围;
的取值范围;
(2)求出函数图像交点M的坐标并指出该点坐标的实际意义;
(3)求甲、乙两车从各自出发地驶出后经过多长时间相遇.
已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1)如图1, 连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请说明理由,若不正确请举反例说明;
(2)若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.



 ,则a+b= ;
,则a+b= ; ;
; 

 的图象交点为C(m,4)求:
的图象交点为C(m,4)求: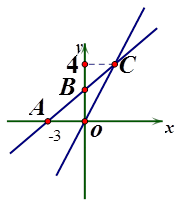
 粤公网安备 44130202000953号
粤公网安备 44130202000953号