北京市朝阳区高三上学期期中统一考试理科数学试卷
已知命题 :
: ,
, ;命题
;命题 :
: ,
, .则下列判断正确的是( )
.则下列判断正确的是( )
A. 是假命题 是假命题 |
B. 是真命题 是真命题 |
C. 是真命题 是真命题 |
D. 是真命题 是真命题 |
设 是两个非零的平面向量,下列说法正确的是( )
是两个非零的平面向量,下列说法正确的是( )
①若 ,则有
,则有 ;
;
② ;
;
③若存在实数λ,使得 =λ
=λ ,则
,则 ;
;
④若 ,则存在实数λ,使得
,则存在实数λ,使得 =λ
=λ .
.
| A.①③ | B.①④ | C.②③ | D.②④ |
某房地产公司计划出租70套相同的公寓房.当每套房月租金定为3000元时,这70套公寓能全租出去;当月租金每增加50元时(设月租金均为50元的整数倍),就会多一套房子不能出租.设租出的每套房子每月需要公司花费100元的日常维修等费用(设租不出的房子不需要花这些费用).要使公司获得最大利润,每套房月租金应定为 ( )
| A.3000 | B.3300 | C.3500 | D.4000 |
如图,某地一天中6时至14时的温度变化曲线近似满足函数 (其中
(其中  ,
, ),
),
|
则估计中午12时的温度近似为( )

A.30 ℃ B.27 ℃ C.25 ℃ D.24 ℃
设函数 满足下列条件:
满足下列条件:
(1)对任意实数 都有
都有 ;
;
(2) ,
, ,
, .
.
下列四个命题:
① ;
;
② ;
;
③ ;
;
④当 ,
, 时,
时, 的最大值为
的最大值为 .
.
其中所有正确命题的序号是( )
| A.①③ | B.②④ | C.②③④ | D.①③④ |
如图,在水平地面上有两座直立的相距60 m的铁塔 和
和 .已知从塔
.已知从塔 的底部看塔
的底部看塔 顶部的仰角是从塔
顶部的仰角是从塔 的底部看塔
的底部看塔 顶部的仰角的2倍,从两塔底部连线中点
顶部的仰角的2倍,从两塔底部连线中点 分别看两塔顶部的仰角互为余角.则从塔
分别看两塔顶部的仰角互为余角.则从塔 的底部看塔
的底部看塔 顶部的仰角的正切值为 ;塔
顶部的仰角的正切值为 ;塔 的高为 m.
的高为 m.
(本小题满分13分)已知函数 (
( )的图象经过点
)的图象经过点 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)求函数 的最小正周期和单调递减区间.
的最小正周期和单调递减区间.
(本小题满分13分)如图,在△ 中,
中, 为钝角,
为钝角, .
. 为
为 延长线上一点,且
延长线上一点,且 .
.
(Ⅰ)求 的大小;
的大小;
(Ⅱ)求 的长及△
的长及△ 的面积.
的面积.
(本小题满分13分)在递减的等比数列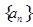 中,设
中,设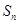 为其前
为其前 项和,已知
项和,已知 ,
,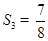 .
.
(Ⅰ)求 ,
,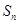 ;
;
(Ⅱ)设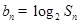 ,试比较
,试比较 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.
(本小题满分14分)已知函数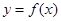 ,若在区间
,若在区间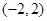 内有且仅有一个
内有且仅有一个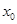 ,使得
,使得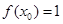 成立,则称函数
成立,则称函数 具有性质
具有性质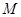 .
.
(Ⅰ)若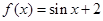 ,判断
,判断 是否具有性质
是否具有性质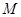 ,说明理由;
,说明理由;
(Ⅱ)若函数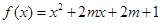 具有性质
具有性质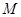 ,试求实数
,试求实数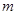 的取值范围.
的取值范围.
 ,则集合
,则集合 等于( )
等于( )



 的值是( )
的值是( )
 与直线
与直线 及
及 轴所围成的图形的面积是( )
轴所围成的图形的面积是( )



 满足
满足 ,
, ,且
,且
 ,则向量
,则向量 的坐标是_______.
的坐标是_______. ,
,  ,则
,则 的值是_______;
的值是_______; 的值是_______.
的值是_______. 是奇函数,则
是奇函数,则 的值是_______.
的值是_______. 中,
中,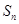 为其前
为其前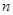 项和.若
项和.若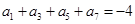 ,
,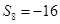 ,则公差
,则公差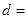 _______;数列
_______;数列 ,
, 满足条件
满足条件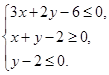 若目标函数
若目标函数 (其中
(其中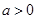 )仅在点
)仅在点 处取得最大值,则
处取得最大值,则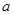 的取值范围是 .
的取值范围是 . .
. 的单调区间;
的单调区间;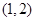 上是单调函数,求
上是单调函数,求 的取值范围.
的取值范围. 的有穷数列
的有穷数列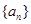 ,记
,记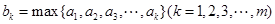 ,即
,即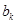 为
为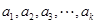 中的最大值,则称
中的最大值,则称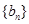 是
是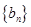 为
为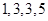 ,写出所有的
,写出所有的 ,
, ,其中
,其中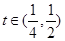 ,
,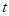 表示
表示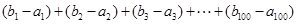 的值;
的值; 的所有全排列中,将每种排列视为一个数列,对于其中控制阶数为2的所有数列,求它们的首项之和.
的所有全排列中,将每种排列视为一个数列,对于其中控制阶数为2的所有数列,求它们的首项之和. 粤公网安备 44130202000953号
粤公网安备 44130202000953号