初中物理计算题

已知煤气的热值为3.6×10⁷J/m³，0.28m³的煤气完全燃烧放出的热量是多少？若这些热量的50%被温度为20℃，质量为30kg的水吸收，则水温升高多少？[c_水=4.2×10³J/(kg·℃)]

美国研制出“会飞的汽车”，如图所示，其车身和一般汽车相似，但车门多了两个可折叠的翅膀，在陆地行驶时，翅膀折叠，在空中飞行时，翅膀张开。汽车的质量为600 kg，地面最大行驶速度可达150 km／h，轮胎与地面接触的总面积约为0.12 m²，空中最大飞行速度可达200 km／h，发动机功率为75 kW。问：

(1)该汽车在地面以最大行驶速度匀速行驶0.2 h，通过的距离是多少?
(2)该汽车静止在水平地面上时，对地面的压强是多少?
(3)若汽车在空中以最大飞行速度匀速飞行200 km，汽车受到的牵引力是多少?

小李同学爱学习，爱家乡，立志为祖国的强盛贡献自己的力量。最近，他向全班同学推荐了两则新闻：
新华网2013年3月19日报道，浙江大学的科学家们研制出了一种超轻材料，这种被称为“全碳气凝胶”的固态材料密度为0.16毫克每立方厘米，刷新了世界纪录。如图21所示。用该材料制成的体积为8立方厘米的“碳海绵”放置在鲜花上。
成都全搜索新闻网2013年5月2日报道，5月2日下午，成都开展了“二环路改造工程主线高架桥标准段结构极限承载能力模型试验研究”。根据测试结果，桥墩所受总荷载达到了2800吨，约为正常设计的4.3倍。
小李同学根据上述两则新闻，编制了下面的计算题，请大家一起来完成。
（1）求8立方厘米“全碳气凝胶”的质量为多少克？
（2）如果将质量为2800吨的物体放在水平地面上，物体与地面的接触面积为28平方米，求物体对地面的压强（g取10N/kg）？

物体在20牛的水平拉力作用下沿拉力的方向做匀速直线运动，5秒内前进了3米。求此过程中拉力做的功W和功率P。

物体排开水的体积为2×10^－3m3，求它所受的浮力F_浮。

甲乙两地的距离是900km，一列火车从甲地早上7:30出发开往乙地，途中停靠了几个车站，在当日16:30到达乙地。列车行驶途中以144km/h的速度匀速通过长度为400m的桥梁，列车全部通过桥梁的时间是25s。求：
（1）火车从甲地开往乙地的平均速度是多少千米每小时？
（2）火车的长度是多少米？

某教师用“试管爬升”实验验证大气压的存在，其做法如下：取两个直径相差很小的平底试管，将细试管底部插入装满水的粗试管内，再将两试管迅速倒置（保持竖直），会看到细试管慢慢“爬进”粗试管里，如图23所示，细试管能否在粗试管内竖直向上“爬升”，取决于开始时插入粗试管的深度，如果插入过浅细试管就不能自动上升。若细试管的重为G，外直径为d，水的密度为ρ₀，大气压强为p₀,请你通过推导计算，回答下列问题：
（1）细试管在“爬升”时，受到大气对它竖直向上的压力是多少？
（2）细试管开始插入的深度h₀满足什么条件时，它刚好可以向上“爬升”。

张先生驾车从广州到肇庆旅游，汽车以90Km/h的平均速度行驶0.5h到达三水，休息0.5h后，再以80Km/h的平均速度行驶1h到达肇庆。请求：
（1）广州到三水，汽车行驶的路程是多少Km？
（2）广州到肇庆，汽车的平均速度是多少Km/h？

在一次测定大气压的实验中，观察到水银柱的高度约为76cm。经计算，当时的大气压近似为10⁵Pa。这样的大气压可支持多高的水柱?(取g="10N/kg)"

三峡水电站的水坝高185m,当水库水位为175m时,坝底受到水的压强是多大?（g=10N/kg）

上海自主研发了一种氢燃料汽车，它使用氢气代替汽油。在一次测试中，汽车在水平路面受到2400N的水平牵引力，5min内匀速直线行驶了9000m。
（1）汽车受到水平方向的阻力是多少？
（2）汽车牵引力所做的功和功率是多少

质量为40kg的小明同学骑着一辆质量为10kg自行车在平直公路上匀速行驶，在5min内行驶了1500m的路程．小明骑自行车与地面总的接触面积为20cm²，则该同学骑车行驶时：

（1）对地面的压力为多少？
（2）对地面的压强为多少？

王洪同学参加学校举行的跳绳比赛，他1min跳了120次，每次跳起的高度为5cm已知他的质量是40kg，求：
（1）王洪同学每次跳起时需要做多少功？
（2）王洪同学跳绳是的功率是多少？

“海宝”是2010年世博会的吉祥物，其形象如图14所示，再点缀上海街头的各种“海宝”中，有一座“海宝”（材质均匀、实心）的体积是2m³密度为1.5×10³kg/m³,与水平地面的接触面积为1m².求：

（1）这座“海宝”的质量m
（2）这座“海宝”的重力大小G
（3）这座“海宝”对地面的压强P

放置在水平地面上的两个物体A和B均为实心长方体，它们的长、宽、高如下图所示。物体A的密度为0.8×10³kg/m³，物体B的质量为8kg。求：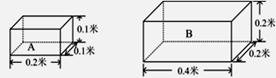

（1）物体A的质量；
（2）物体B所受重力的大小；
（3）在保持物体A、B原有放置方式的情况下，若沿竖直方向截取物体，并通过一定的方法使它们对水平地面的压强相等。下表中有两种方案，请判断这两种方案是否可行，若认为可行，计算所截取的长度。

	内　　容	判断（填“行”或“不行”）
方案一	从A的右侧截取一部分长方体叠放在B的上表面
方案二	分别从A、B的右侧按相同比例截取一部分长方体，叠放在对方剩余部分的上表面