初中物理超纲知识综合题

电容器是电气设备中的重要元件，是储存电荷的装置。两个相距很近又彼此绝缘的平行金属板就形成一个最简单的电容器。在电路图中用符号“”表示。

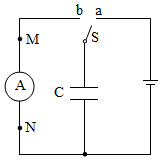
（1）如图电路，开关置于 $a$时，电容器的一个极板与电源的正极相连，另一个极板与负极相连，两个极板将分别带上等量异种电荷，这个过程叫做电容器充电，电容器一个极板所带电荷量的绝对值叫做电容器所带的电荷量。开关置于 $b$时，充电后的电容器的两极板接通，两极板上的电荷中和，电容器又不带电了，这个过程叫做电容器放电。放电过程中，经过电流表的电流方向为　       　（选填“ $M$到 $N$或“ $N$到 $M$” $)$

（2）当开关置于 $a$时，通过改变电源电压来改变电容器两极板间的电压 $U$，电容器所带的电荷量 $Q$也随之改变。实验数据如表：

次数	1	2	3	4
电压	4.0	8.0	12.0	16.0
电荷量 $Q/C$	$4.04\times {10}^{-3}$	$8.00\times {10}^{-3}$	$12.14\times {10}^{-3}$	$16.32\times {10}^{-3}$
$\frac{Q}{U}/(C$． $V^{-1})$	$1.01\times {10}^{-3}$	$1.00\times {10}^{-3}$	$1.01\times {10}^{-3}$	$1.02\times {10}^{-3}$

实验表明，在误差允许的范围内，这个电容器所带的电荷量 $Q$与两极板间的电压 $U$的比值是一个常量。换用不同的电容器，这个比值一般是不同的。

电容器所带的电荷量 $Q$与两极板间电压 $U$的比值叫做电容器的电容，用符号 $C$表示，表达式为 $C=\frac{Q}{U}$．在国际单位制中，电容的单位是法拉，符号是 $F$． $1F=1C/V$

①电容器两极板间电压减小，它的电容　        　。

②上述电路中，若电源电压为 $9V$，换用电容为 $3.0\times {10}^{-12}F$的电容器，充电完毕后再进行放电，在全部放电过程中释放的电荷量是　         　库。

演绎式探究 $---$探究点电荷的电场强度

如果带电体间的距离比它们的大小大得多，这样的带电体可以看成是点电荷。

（1）实验发现，带电量分别为 $q_1$、 $q_2$的两个点电荷距离为 $r$时，它们之间的作用力 $F=k\frac{q_1{q}_2}{r^2}$，其中 $k$为常量，当 $q_1$和 $r$一定时， $F$与 $q_2$之间的关系图象可以用图甲中的图线　　来表示。

（2）磁体周围存在磁场，同样，电荷周围也存在磁场。电场对放入其中的电荷产生电场力的作用。点电荷 $q_1$和 $q_2$之间的作用力实际是 $q_1$（或 $q_2)$的电场对 $q_2$（或 $q_1)$的电场力。物理学中规定：放入电场中某一点的电荷受到的电场力 $F$跟它的电量 $q$的比值，叫做该点的电场强度，用 $E$表示，则 $E=$　　。

如图乙所示，在距离点电荷 $Q$为 $r$的 $A$点放一个点电荷 $q$，则点电荷 $q$受到的电场力 $F=$　　，点电荷 $Q$在 $A$点产生的电场强度 $E_A=$　　。

（3）如果两个点电荷同时存在，它们的电场会相互叠加，形成合电场。

如图丙所示，两个互成角度的电场强度 $E_1$和 $E_2$，它们合成后的电场强度 $E$用平行四边形的对角线表示。如图丁所示，两个点电荷 $Q$分别放在 $A$、 $B$两点，它们在 $C$点产生的合电场强度为 $E_{合}$．请推导证明： $E_{合}=\sqrt{2}\frac{\mathit{kQ}}{r{}^2}$。

演绎式探究 $-$探究太阳的引力系数：

（1）宇宙中任何两个物体之间都存在万有引力，万有引力的大小 $F_{引}=G\frac{m_1{m}_2}{r^2}$，其中 $m_1$、 $m_2$分别为两个物体间的距离，万有引力常数 $G=6.67\times {10}^{-11}N·m^2/k{g}^2$．物体间引力和距离一定时，两个物体质量 $m_1$、 $m_2$分的关系可以用如图中图线　 $b$　来表示。

（2）行星绕恒星的运动可以近似地看作匀速圆周运动。行星受到一个恒定的指向恒星的向心力，向心力的大小 $F_{向}=m{\omega }^{2}r$，其中 $m$为行星质量， $r$为两星之间的距离， $\omega$为行星做圆周运动的角速度，其大小等于单位时间内行星与恒星连线转过的角度。行星绕恒星运动一周所用的时间用周期 $T$表示，角速度 $\omega$与转动周期 $T$的关系为： $\omega =\frac{2\pi }{T}$．行星所受向心力 $F_{向}$的大小等于恒星对行星的引力 $F_{引}$的大小。

每个星球对在它表面附件的物体都存在引力，引力与物体质量的比值叫作引力系数，用 $g$表示，我们学过地球的引力系数 $g_{地}=10N/\mathit{kg}$。对于每个星球来讲，下列公式成立： $R^{2}g=\mathit{GM}$，其中 $R$为星球半径， $g$为星球引力系数， $M$为星球质量，万有引力常数 $G=6.67\times {10}^{-11}N·m^2/k{g}^2$。

已知地球质量为 $m$，地球到太阳的距离为 $L$，太阳半径为 $R$，地球的公转周期为 $T$．请你推导出太阳的引力系数 $g_{日}=\frac{4{\pi }^2{L}^3}{R^2{T}^2}$。