小明将一箱器材搬到三楼的实验室,准备采用两种方法:一是将这箱器材一次性搬上楼,他做的有用功是W1,此方法做功的机械效率为η1;二是将这箱器材先搬一部分上楼,再搬剩下部分。他做的有用功是W2,此种方法做功的机械效率为η2。假设他上楼的速度相同,则两种方法中的有用功和机械效率的关系分别是( )
| A.W1<W2η1<η2 |
| B.W1=W2 η1<η2 |
| C.W1<W2η1>η2 |
| D.W1=W2η1>η2 |
为了将放置在水平地面上重为100N的物体提升一定高度,设置了图所示的滑轮组装置。当用图甲所示随时间变化的竖直向下的拉力F拉绳时,物体的速度v和物体上升的高度h随时间变化的关系分别如图乙和丙所示。(不计绳重和绳与轮之间的摩擦)下列计算结果正确的是( )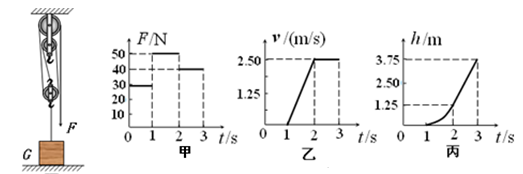
| A.0s~1s内,地面对物体的支持力是10N |
| B.1s~2s内,拉力F做的功是187.5J |
| C.2s~3s内,拉力F的功率是100W |
| D.2s~3s内,滑轮组的机械效率是62.5% |
建筑工地上,起重机几分钟内就能把所需的砖送到楼顶,如果人直接用滑轮组来提升则需要几个小时,其原因是( )
| A.起重机的功率大,做功多 |
| B.起重机的机械效率高,做功慢 |
| C.起重机的功率大,做功快 |
| D.起重机的机械效率高,做功多 |
利用等重滑轮,分别采用如图所示的两种方式提升同一重物,升高相等高度。若绳重和摩擦不计,下列分析中正确是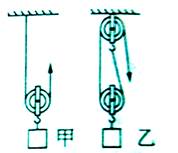
| A.乙绳自由端移动距离较大 |
| B.乙绳自由端作用力较小 |
| C.两种方式所做额外功相等 |
| D.增大提升高度效率都变大 |
工人用滑轮组把一箱箱货物从一楼提升到五楼,在滑轮组上加润滑油后,机械效率提高了,则加润滑油后工人提升同样的重物时,做的 ( )
| A.有用功减小,总功不变 | B.有用功增加,总功增加 |
| C.有用功不变,总功减小 | D.有用功减小,总功减小 |
小明用两个相同的滑轮,组成不同的滑轮组(如图所示),分别将同一物体匀速提高到相同高度,绳子的自由端移动的距离为S1、S2,图中左、右滑轮组的机械效率分别为η1、η2。下列关系正确的是(忽略绳重及摩擦)( )
| A.S1>S2,η1=η2 | B.S1>S2,η1>η2 |
| C.S1<S2,η1=η2 | D.S1<S2,η1>η2 |
如图,小明分别用甲、乙两个滑轮把同一袋沙子从地面提到二楼,用甲滑轮所做的总功为W1,机械效率为η1;用乙滑轮所做的总功为W2,机械效率为η2.若不计绳重与摩擦,则( )

| A.W1=W2 η1=η2 | B.W1<W2 η1<η2 |
| C.W1>W2 η1>η2 | D.W1<W2 η1>η2 |
工人用如图所示的滑轮组将重为500N的物体在4s内匀速提升了2m,若每个滑轮重40N,不计绳重和摩擦,则在此过程中,下列说法正确的是
| A.绳端的拉力F为270N | B.拉力F的功率为270W |
| C.额外功为160J | D.有用功为1080J |
关于功、功率、机械效率说法正确的是( )
| A.功率越大,反映做功越快,与机械效率无关 |
| B.做功越少,功率越小,机械效率越小 |
| C.功率越大,做功越快,机械效率越大 |
| D.机械效率越大,表明它做的功越多 |
从井中提水时,常常会发生吊水桶落入井里的事情.用物理知识分析下列说法,其中错误的是( )
| A.用吊水桶向上提水,人对桶和水做的功都是有用功 |
| B.用吊水桶向上提水,人对桶做的功是额外功 |
| C.吊水桶掉在井里,打捞水桶时桶里会带些水,这时人对水做的功是额外功 |
| D.吊水桶掉在井里,打捞水桶时,人对桶做的功是有用功 |
分别用如图所示的甲、乙两个滑轮组,在100s内将重为400N 的物体G匀速提升10m,每个滑轮的重均为20N.不计绳重及摩擦,此过程中( )
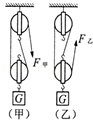
| A.拉力F甲小于拉力F乙 |
| B.F甲做的功小于F乙做的功 |
| C.滑轮组甲的机械效率小于滑轮组乙的机械效率 |
| D.F甲做功的功率等于F乙做功的功率 |
某实验小组分别用如图所示的甲、乙两个滑轮组(每个滑轮重相同)匀速提起相同的重物.不计绳重及摩擦,下列说法正确的是( )

| A.甲图省力,机械效率一样大 |
| B.甲图省力,机械效率甲图大 |
| C.乙图省力,机械效率一样大 |
| D.乙图省力,机械效率乙图大 |
如图(不计绳重与摩擦,且动滑轮重G动小于物重G),用它们分别将重相同的甲、乙两物体匀速提升相同的高度,所用的拉力分别为F甲、F乙,它们的机械效率分别为η甲、η乙。则下列关系正确的是( )

| A.F甲<F乙 | B.F甲=F乙 [来源 | C.η甲>η乙 | D.η甲 =η乙 |
已知甲、乙两种机械在做功过程中,甲的机械效率比乙的机械效率大,这表明( )
| A.甲做功比乙做功快 |
| B.甲做的有用功比乙做的有用功多 |
| C.甲做的额外功比乙做的额外功少 |
| D.甲做的有用功,与总功的比值比乙大 |