用图所示的装置来测滑轮组的机械效率。
(1)实验要求,用弹簧测力计拉动绳端时,拉力的方向应 ,并使物体 上升。
(2)若弹簧测力计移动15cm,则物体移动 m。
(3)若在实际的实验中,物体上升10cm,弹簧测力计上升30cm,被提升的物体总重为6N,动滑轮重为0.5N,弹簧测力计读数是2.5N,则拉力做的额外功是 J。滑轮组的机械效率是 。
(4)若再加挂一只钩码重做实验,所测的机械效率与前一次相比将 。(选填“相同”或“变大”或“变小”)。
已知甲、乙两种机械在做功过程中,甲的机械效率比乙的机械效率大,这表明 ( )
| A.甲做功比乙做功快 |
| B.甲做的有用功比乙做的有用功多 |
| C.甲做的额外功比乙做的额外功少 |
| D.甲做的有用功与总功的比值比乙大 |
关于功率,下列说法正确的是( )
| A.做功多的机器,功率一定大 |
| B.做功时间短的,功率一定大 |
| C.做相同的功,所用时间短的,功率一定大 |
| D.以上说法都不对 |
某实验小组在“测滑轮组机械效率”的实验中得到的数据如下表所示,第1、2、3次实验装置分别如图中的甲、乙、丙所示。 
(1)第3次实验中所做的有用功是 J,机械效率是 
(2)比较第1次实验和第2次实验,可得结论:
。
(3) 比较第2次实验和第3次实验,可得结论:
。
(4)可见,提高机械效率的方法有增大有用功,
额外功(选填“增大”或“减小”)。
针对“斜面的倾斜程度与斜面的机械效率有怎样的关系?”这个问题,某同学利用同一木板,搭成不同倾角的斜面,将同一小车沿斜面匀速拉动,记录实验数据如下表。
| 实验 次数 |
斜面倾 斜程度 |
小车重 G/N |
小车上升 高度h/m |
沿斜面 拉力F/N |
小车移动 距离S/m |
有用功 W/J |
总功W/J |
机械 效率η |
| 1 |
较缓 |
4.0 |
0.2 |
0.9 |
1.2 |
0.8 |
1.08 |
74% |
| 2 |
较陡 |
4.0 |
0.3 |
1.2 |
1.2 |
1.2 |
1.44 |
83% |
| 3 |
最陡 |
4.0 |
0.4 |
1.5 |
1.2 |
1.6 |
|
|
(1)请你将该同学第3次的实验数据填入表格中。
(2)分析实验数据可知,在粗糙程度相同的情况下,斜面的省力情况与斜面倾斜程度的关系是: 。
(3)分析实验数据可知:在粗糙程度相同的情况下,斜面的机械效率与斜面倾斜程度的关系是: 。
(4)如果该同学还要进一步探究“斜面的机械效率与物重的关系”,实验时应控制小车移动的距离、 和 不变。
在生产和生活中,经常见到这样的情形:用木板搭斜坡将货物推上汽车车厢;修盘山公路使汽车驶上高耸的山峰等。从物理学的角度分析,它们的物理模型属于同一种简单机械,即__________,这种简单机械的优点是__________。
下列过程中,动能转化为势能的是( )
| A.重锤从高处落下 | B.钟表里的发条带动齿轮转动 |
| C.压缩的弹簧将物体弹射的瞬间 | D.炮弹从炮口斜向上射出去 |
利用如图所示的滑轮组把重180N的物体匀速提高10m,已知滑轮组机械效率是80%(不计绳重和摩擦),求:
(1)提升重物时做的有用功为多少?
(2)作用在绳子自由端的拉力为多大?
(3)用此滑轮组匀速吊起重为455N的物体时,滑轮组的机械效率是多大?
“神州六号”载人飞船成功地将航天员费俊龙、聂海胜送上太空遨游并随返回舱一起返回.为了使快速降落的返回舱安全着陆,在距离地面的一定高度,点燃反推火箭发动机向下喷出高温高压气体,从开始喷气到安全着陆,返回舱的动能________,重力势能________(选填“增大”、“减小”或“不变”)。
甲站在0.5m/s匀速上行的自动扶梯上,乙站在0.7m/s匀速下行的自动扶梯上.甲、乙两人质量相等,甲上行中动能 (选填“增加”、“不变”、“减少”).某时刻他们的位置如图所示,该时刻甲的重力势能 乙的重力势能,甲的机械能 乙的机械能.(选填“大于”、“等于”、“小于”).若此时上行的扶梯突然停止运动,甲会向前倾,原因是 。
蹦床运动是运动员从蹦床弹向空中表演技巧动作的一项体育活动。当运动员离开蹦床弹向空中的过程中,运动员具有的( )
| A.动能增加,势能减少 | B.动能增加,势能增加 |
| C.动能减少,势能减少 | D.动能减少,势能增加 |
如图所示,重为10N的物体G挂在水平杠杆的A端(杠杆重力不计),要使杠杆在图示位置平衡,在B端至少要施加__________N的力,力的方向是______________。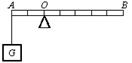
工人站在地上,利用图所示的滑轮组把重物提升到楼上,请在图中画出滑轮组的绕绳方法。
有下列四种杠杆:手推车、筷子、起重机吊臂,属于费力杠杆的有 (填写序号),属于省力杠杆的有 (填写序号). 人们修建盘山公路的目的是为了 .