在图所示的装置中DC=3m,OD=1m,A、B两个滑轮的质量均为2kg,A是边长为20 cm、密度为 的正方体合金块,当质量为60kg的人用
的正方体合金块,当质量为60kg的人用 80N的力沿竖直方向向下拉绳时,合金块A全部浸没在密度为
80N的力沿竖直方向向下拉绳时,合金块A全部浸没在密度为 的液体中,杠杆恰好在水平位置平衡,此时人对地面的压强为
的液体中,杠杆恰好在水平位置平衡,此时人对地面的压强为 ;若人缓慢松绳,使合金块下降并与容器底接触(但不密合),当人用
;若人缓慢松绳,使合金块下降并与容器底接触(但不密合),当人用 60N的力向下拉绳时,人对地面的压强为
60N的力向下拉绳时,人对地面的压强为 ,容器底对A的压强为
,容器底对A的压强为 。 (杠杆DC的质量不计,
。 (杠杆DC的质量不计, 、
、 )
)
求:(1)液体的密度 ;(2)
;(2) 。
。
如图是某同学设计的简易打捞装置结构示意图。AOB是以O点为转轴,长为4m的轻质横梁, AB呈水平状态,AO=1m。在横梁上方行走装置可以在轨道槽内自由移动,行走装置下方固定有提升电动机。提升电动机通过细绳和滑轮组提起重物。固定在水平地面上的配重T通过细绳与横梁A端相连,GT=3000N。当行走装置处于C位置时,开始打捞物体A。质量mA是100kg、体积V为0.04m3 物体A在水中匀速上升时,地面对配重T的支持力是N1,滑轮组的机械效率为75%;当物体A全部露出液面,滑轮组将物体A以v是0.1m/s的速度匀速竖直向上提升1m,此时电动机拉动细绳的功率为P,地面对配重T的支持力是N2;N1∶N2=5∶1,若行走装置和提升电动机及定滑轮的总质量m2是20kg,,忽略细绳与滑轮的摩擦以及水对物体的阻力,g取10N/kg。求
(1)动滑轮的重力G动
(2)电动机拉动细绳的功率P
(3)OC的距离
如图所示 支撑杠杆水平平衡的支架AOB随物体M在液体中能上下运动自动升降,物体M的密度为2.7×103kg/m3,轻质杠杆LOA∶LOB=2∶5。某同学质量为60kg,利用这个装置进行多次实验操作,并将实验数据记录于表格中(表格中F浮为物体所受的浮力、h为物块浸入液体的深度,P为液体对容器底部的压强),在各次操作过程中可认为杠杆始终保持水平。其中一次实验用力F1拉动绳自由端匀速竖直向下运动,该同学对地面的压强为独立站在地面时对地压强的一半,滑轮组的机械效率η=90%。已知,物体M浸没在液体中时,液体深度1.8m(绳的重力、滑轮与轴的摩擦及液体对物体的阻力不计。g=10N/kg)。
| F浮/ N |
100 |
200 |
300 |
400 |
500 |
600 |
600 |
600 |
| h/m |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
| P/ pa |
16725 |
16975 |
17225 |
17425 |
17725 |
18000 |
18000 |
18000 |

求:
(1)拉力F1的大小;
(2)液体的密度;
(3)物体M完全露出液体表面时,滑轮组的机械效率(百分号前面保留整数);
如图甲所示,B是一个固定支架,由立柱和两侧装有定滑轮的水平横梁组成,物体M在横梁上可左右移动,M的左端用钢绳跨过定滑轮与电动机相连,右端用钢绳跨过定滑轮与滑轮组相连,滑轮组下挂一实心物体A,其密度ρA=5×103kg/m3,体积VA=0.024m3。当电动机不工作时(可视电动机对钢绳无拉力作用),将物体A浸没在水中,物体A可以通过滑轮组拉着物体M向右匀速运动;当电动机用一个竖直向下的力F1拉钢绳时,物体A在水面下以速度υ1=0.1m/s匀速上升,滑轮组的机械效率为η1;当物体A完全露出水面后,电动机用力F2拉钢绳,物体A匀速上升,滑轮组的机械效率为η2。在以上过程中,电动机对钢绳的拉力的大小随物体A上升高度的关系如图乙所示,电动机以F1、F2拉钢绳时的功率始终为P。(不计钢绳的质量、滑轮与轴的摩擦、水对物体的阻力。取g =10N/kg)
求:
(1)滑轮组的机械效率η1:η2
(2)电动机的功率P
建筑工人使用如图所示装置,将质量分布均匀的长方体水泥板M吊起后放入水中。工人通过控制电动机A、电动机B,始终保持水泥板M所受拉力竖直向上。当电动机A对绳的拉力为零时,电动机A对地面的压强为p0;当水泥板M一端被竖直滑轮组拉起,另一端仍停在地面上,且水泥板M与水平地面成某角度时,电动机A对地面的压强为p1;当水泥板M被竖直滑轮组拉离地面时,电动机A对地面的压强为p2;当将水泥板M被悬挂着浸没在水中时,电动机A对地面的压强为p3。已知:水泥板M的体积VM为0.1m3, =
= =5250Pa,
=5250Pa, =
= =10250Pa,
=10250Pa, =
= =5250Pa,不计绳重和轴摩擦。(g取10N/kg)求:
=5250Pa,不计绳重和轴摩擦。(g取10N/kg)求:
(1)竖直滑轮组中动滑轮的总重力G动 ;
(2)水泥板M所受重力GM;
(3)竖直滑轮组提拉水泥板M将其立起的过程中机械效率η。(结果保留两位有效数字)
如图所示,是使用汽车打捞水下重物的示意图。汽车通过滑轮组打捞水下一个圆柱形重物,在整个打捞过程中,汽车以0.3m/s的速度向右水平匀速运动。重物在水面下被提升的过程共用时50s,汽车拉动绳子的功率P1为480W。重物开始露出水面到完全被打捞出水的过程共用时10s,此过程中汽车拉动绳子的功率逐渐变大,当重物完全被打捞出水后,汽车的功率P2比P1增加了120W,且滑轮组机械效率为80%。忽略水的阻力、绳重和滑轮的摩擦,g取10N/kg。求: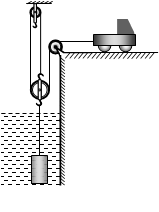
(1)重物浸没在水中所受浮力;
(2)打捞前重物上表面受到水的压力;
(3)被打捞重物的密度
今年小明家种植柑橘获得了丰收。小明想:柑橘的密度是多少呢?于是,他将柑橘带到学校实验室,用天平、溢水杯来测量柑橘的密度。他用天平测出一个柑橘的质量是114g,又用溢水杯测出了一个柑橘的体积是120 cm3。小明测体积的方法是:先用天平称出装满水的溢水杯的总质量是360g,然后借助铅笔使这个柑橘浸没在溢水杯中,当溢水杯停止排水后再取出柑橘,接着测得溢水杯的总质量是240g,然后他算出了一个柑橘的体积V橘=V排=m排/ρ水=120 g/1.0 g/cm3=120 cm3 。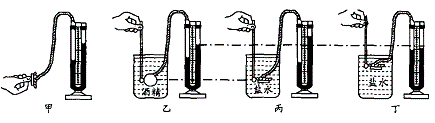
请根据上述实验过程解答下列问题:
(1)溢水杯中排出水的质量是多大?浸没在水中的柑橘受到的浮力是多大?
(2)这个柑橘的密度是多大?
(3)小明用这种方法测出的这个柑橘的密度与它的实际密度比较,是偏大还是偏小?为什么?
科技小组的同学用泡沫塑料和灯泡等物件制作了一个航标灯模型,如右图A所示.航标灯A总重4 N,A底部与浮子B用细绳相连.当水位上升时,浮子B下降;水位下降时,浮子B上升,使航标灯A静止时浸入水中的深度始终保持为5 cm,航标灯A排开水的质量为500 g、浮子B重0.5 N(不计绳重和绳与滑轮之间的摩擦).求:
(1)是多大?
(2)航标灯静止时,浮子B的体积应为多大?(g取10 N/kg,ρ水=1.0×103 kg/m3)
某人用绳子将一物体从水面下2m深处的地方匀速提到水面0.5m处的过程中,人对物体做功为54J.当将物体拉到有 体积露出水面时,让其静止,此时绳子对物体的拉力为40N.不计绳子的质量,忽略水的阻力,求物体的密度.(g取10N/kg)
体积露出水面时,让其静止,此时绳子对物体的拉力为40N.不计绳子的质量,忽略水的阻力,求物体的密度.(g取10N/kg)
示轻质杠杆,把密度均为4.0×103kg/m3的甲、乙两个实心物体挂在A、B两端时,杠杆在水平位置平衡,若将甲物体浸没在水中,同时把支点从O移到O′时,杠杆又在新的位置平衡,若两次支点的距离O O′为OA的 ,求:甲、乙两个物体的质量之比.
,求:甲、乙两个物体的质量之比.
图1—5—19
图1—5—13(a),在天平左盘放一杯水,右盘放砝码,使天平平衡.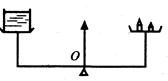
(a) (b)
图1—5—13
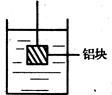
(1)将一质量为27g的铝块(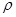 铝=2.7g/m3)放入左盘水中,水不溢出,天平还能平衡吗?
铝=2.7g/m3)放入左盘水中,水不溢出,天平还能平衡吗?
(2)将铝块如图1—5—13(b)方式放入左盘中,天平还能平衡吗?
面积为400cm2的圆柱形容器内装有适量的水,将其竖直放在水平桌面上,把边长为10cm的正方体木块A放入水后,再在木块A的上方放一物体B,物体B恰好没入水中,如图1—5—11(a)所示.已知物体B的密度为6×103kg/m3.质量为0.6kg.(取g=10N/kg)

(a) (b)
图1—5—11
求:(1)木块A的密度.
(2)若将B放入水中,如图(b)所示,求水对容器底部压强的变化.
已知:S=400cm2=0.04m2,A边长a=10cm=0.1m, B=6×103kg/m2,mB=0.6kg
B=6×103kg/m2,mB=0.6kg
求:(1)pA;(2)△p.
图1—5—8所示的木块浸没在水中,细线对木块的拉力是2N.剪断细线,待木块静止后,将木块露出水面的部分切去,再在剩余的木块上加1N向下的压力时,木块有20cm3的体积露出水面.求木块的密度.(g取10N/kg) 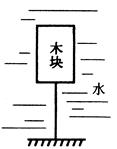
图1—5—8
图1—5—7所示,把甲铁块放在木块上,木块恰好浸没于水中,把乙块系在这个木块下面,木块也恰好浸没水中,已知铁的密度为7.9×103kg/m3.求:甲、乙铁块的质量比.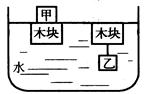
图1—5—7
图1—5—6(a)所示,一个木块用细绳系在容器的底部,向容器内倒水,当木块露出水面的体积是20cm3,时,细绳对木块的拉力为0.6N.将细绳剪断,木块上浮,静止时有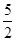 的体积露出水面,如图(b)所示,求此时木块受到的浮力.(g取10N/kg)
的体积露出水面,如图(b)所示,求此时木块受到的浮力.(g取10N/kg)
(a) (b)
图1—5—6