某学生做以下实验:先在一只玻璃水槽中注入一定量的水,后将盛有一些小石子的塑料小船放入水里(如图所示),测得船底到液面的距离为h,再每隔一定时间向水里加食盐并搅动,直至食盐有剩余.问在他所绘制的吃水线至船底距离h随加盐量而变化的图象中(如图所示)正确的是:




A B C D
如图所示,把甲、乙两个体积相同的实心球投入水中,甲球漂浮,乙球悬浮。则( )

| A.乙球的密度是1.0×103千克/米3 |
| B.甲球的密度小于乙球的密度 |
| C.甲球受到的浮力大于它所受的重力 |
| D.乙球受到的浮力比甲球受到的浮力大 |
将一方形木块(体积为V木)放于水中,再将一方形冰块(体积为V冰)放于木块上,静止时水面正好和木、冰交界面共面(如图),已知水、冰、木密度之比为10:9:8,则V冰:V木为(说明:图中冰块、木块大小不具暗示意义)( )

| A.9:8 | B.8:9 | C.1:8 | D.2:9 |
质量相同的甲、乙、丙、丁4个小球,分别静止在水中的不同深度处,如下图所示,则这4个小球在水中所受浮力最小的是
| A.甲 | B.乙 | C.丙 | D.丁 |
如图,小瓷碗漂浮在水面上,倾斜后能沉入水底,关于这一情景分析正确的是( )
| A.小瓷碗能沉入水底是因为它的重力变大了 |
| B.小瓷碗漂浮时受到的浮力等于它的重力 |
| C.小瓷碗浸没时和漂浮时相比所受的浮力变小了 |
| D.小瓷碗浸没后容器底受到水的压强变大了 |
如图(1)所示,边长为10cm的立方体木块A通过细线与圆柱形容器底部相连,容器中液面与A上表面齐平.从打开容器底部的抽液机匀速向外排液开始计时,细线中拉力F随时间t的变化图像如图(2)所示.木块密度ρ = 0.5×103kg/m3,容器底部面积为200cm2,g = 10N/kg.下列说法中正确的是
| A.随着液体的排出,木块受到的浮力不断减小 |
| B.容器中的液体是酒精 |
| C.抽液机每秒钟排出液体的质量是10g |
| D.第 30 s 时,木块露出液面的高度是 2cm |
如图所示,甲图中圆柱形容器中装有适量的水。将密度均匀的木块A放入水中静止时,有2/5的体积露出水面,如图乙所示,此时水对容器底部的压强比图甲水对容器底部的压强增加了300 Pa。若在木块A上表面轻放一个质量为m1的物块,平衡时木块A仍有部分体积露出水面,如图丙所示,此时水对容器底部的压强比图甲水对容器底部的压强增加了400Pa。若将容器中的水换成另一种液体,在木块A上表面轻放一个质量为m2的物块,使平衡时木块A露出液面部分与丙图相同,如图丁所示。若m1∶m2=5∶1,则下列说法中错误的是 
| A.木块A的质量mA与m1之比为1:3 |
B.在丁图中,液体的密度为 kg/m3 kg/m3 |
C.木块A的密度为 kg/m3 kg/m3 |
| D.在图丙中,木块A露出水面的体积与木块A的体积之比是1:5 |
将甲、乙两个完全相同的溢水杯放在水平桌面上,甲溢水杯中装满密度为ρ1的液体,乙溢水杯中装满密度为ρ2的液体。如图8甲所示,将密度为ρA,重为GA的物块A轻轻放入甲溢水杯中,物块A漂浮在液面上,并且有1/4的体积露出液面,液体对甲杯底的压强为P1。如图乙所示,将密度为ρB,重为GB的物块B轻轻放入乙溢水杯中,物块B沉底,物块B对乙溢水杯底的压力为F,液体对乙溢水杯杯底的压强为P2。已知
ρ1∶ρ2=3∶2,ρA∶ρB=4∶5,则下列说法中正确的是
| A.ρ1∶ρA,=3∶4 |
| B.FA浮∶FB浮=9∶8 |
| C.P1∶P2=2∶3 |
| D.F∶GB=13∶45 |
如图甲是一个底面为正方形、底面边长l=20cm的容器。把盛有h=10cm深的某种液体的容器放在水平桌面上,然后将边长a=b=10cm、c=12cm的均匀长方体木块放入这种液体中(液体未溢出),木块漂浮在液面上,此时木块底面受到液体向上的压力为7.2 N,容器底受到的液体压强为980Pa(g取10N/kg),由以上条件可以得出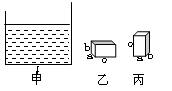
| A.液体的密度为0.98×103kg/m3 |
| B.木块漂浮在液面上时,容器中液体的深度为12.2cm |
| C.以图乙所示方式将木块放入液体中静止时,木块浸入液体中的深度为7.5cm |
| D.以图丙所示方式将木块放入液体中静止时,木块下表面离容器底的距离是4.75cm |
如图所示,两个相同容器盛满水,甲中有一个体积为20cm3,密度为0.5×103kg/m3的木块漂浮在水面.下列说法正确的是( )
A.木块漂浮时,浮力等于自身重力,并有 体积露出水面 体积露出水面 |
| B.甲容器对水平桌面的压力大于乙容器对水平桌面的压力 |
| C.将木块缓慢下压至浸没的过程中,木块受到的浮力不变 |
| D.将木块全部压入水中后,两容器底部受到水的压力相等 |
轻质硬杆AB长50cm。用长短不同的线把边长为10cm的立方体甲和体积是1dm3的球乙分别拴在杆的两端。在距A点20cm处的O点支起AB时,甲静止在桌面上,乙悬空,杆AB处于水平平衡。将乙浸没在水中后,杆AB仍平衡,如图7所示。下列说法中正确的是(取g=10N/kg)
| A.杆A端受力增加了15N |
| B.杆A端受力减小了10N |
| C.甲对水平桌面的压强增加了1500Pa |
| D.甲对水平桌面的压强减小了1500Pa |
在图所示装置中,杠杆和滑轮的重力及滑轮的摩擦均可忽略不计,杠杆AB可以绕O点在竖直平面内自由转动,A端通过竖直方向的轻绳与滑轮组相连,在B端用一轻绳沿竖直方向将杠杆拉住,使其始终保持水平平衡。在滑轮组的下方,悬挂一圆柱形的物体,此物体被浸在圆柱形容器内的液体中。已知杠杆O点两侧的长度关系为AO=2OB,圆柱形物体的底面积为10cm2、高为12 cm,圆柱形容器的底面积为50cm2。若容器中的液体为水,在水深为20cm时物体的上表面恰与水面相平,此时杠杆B端绳上的拉力为F1;打开圆柱形容器下方的阀门K,将水向外释放,直到物体露出水面的体积为其总体积的2/3时,将阀门K关闭,此时杠杆B端绳上的拉力为F2,且F1:F2=3:4。若容器中液体为某种未知液体,其质量与最初容器中的水的质量相等,此时未知液体的深度为18 cm,杠杆B端绳上的拉力为F3。取g=10N/kg,则
| A.圆柱形物体的密度为2 g/cm3 |
| B.作用在B端的拉力F3大小为1.52N |
| C.未知液体的密度为1.2 g/cm3 |
| D.未知液体对圆柱形容器底部的压强为1980Pa |
如图所示,重为100N的物体B,在足够深的水中匀速下沉,通过滑轮组拉着重600N的物体A沿水平方向匀速运动,在4s内物体A移动了0.8米,已知B的密度是水的密度的5倍,动滑轮重12N,不计绳重及滑轮与绳之间的摩擦,g取10N/kg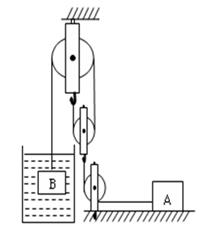
| A.B对绳的拉力是20N |
| B.B对绳的拉力的功率是16W |
| C.A物体受摩擦力为148N |
| D.滑轮组的机械效率为90% |
如图所示,有两只完全相同的溢水杯分别盛有密度不同的A、B两种液体,将两个体积均为V,所受重力分别为GC 、GD的小球C、D分别放入两容器中,当两球静止时,两杯中液面相平,且C球有一半体积浸入液体中,D球全部浸入液体中。此时两种液体对甲、乙两容器底部的压强分别为pA、pB ;甲、乙两容器对桌面的压强分别为p1、p2。要使C球刚好完全没入液体中,须对C球施加竖直向下的压力F,若用与F同样大小的力竖直向上提D球,可使它有V1的体积露出液面。已知C、D两球的密度比为2:3。则下述判断正确的是
A.p1>p2 ;2GC =3GD
B.3p1=4p2 ;pA>pB
C.3GC =2GD;3V1 ="2" V
D.3pA=4pB ;3V1 = V
如图所示,有两个小球M和N,密度分别为ρM和ρN,小球所受重力大小分别为GM和GN,体积分别为VM和VN。将它们用细线分别挂在轻质杠杆AB两端,且小球M浸没在甲杯的水中静止,小球N浸没在乙杯的油中静止,杠杆AB恰能在水平位置平衡。小球M和N所受浮力分别为FM和FN。已知:AO׃OB =1׃2,水的密度为ρ水、油的密度为ρ水,且ρN>ρM>ρ水>ρ油,则下列判断中正确的是 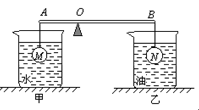
| A.FM<2FN | B.FM>2FN | C.VM>2VN | D.GM>2GN |