如图是吊车起吊货物的结构示意图,伸缩撑杆为圆弧状,工作时它对吊臂的支持力始终与吊臂垂直,使吊臂绕O点缓慢转动,从而将货物提起.下列说法正确的是( )
| A.吊臂是一省力杠杆,但要费距离 |
| B.吊臂是一个费力杠杆,但可以省功 |
| C.匀速顶起吊臂的过程中,伸缩撑杆支持力的力臂变小 |
| D.匀速顶起吊臂的过程中,伸缩撑杆支持力渐渐变小 |
探究杠杆的平衡条件
【提出问题】如图所示,是一种常见的杆秤.此时处于水平位置平衡.
发现一:小明在左侧挂钩上增加物体,可观察到提纽左侧下沉.他认为改变杠杆的水平平衡可以通过改变作用在杠杆上的 来实现;
发现二;接着小新移动秤砣使其恢复水平位置平衡。说明通过改变 的长短也可以改变杠杆的平衡.
那么,杠杆在满足什么条件时才平衡呢?
【制定计划与设计实验】
实验前,轻质杠杆处于如图所示的状态,使用时,首先应将杠杆的平衡螺母向 (选填“左”或“右”)调节,使杠杆处于水平位置平衡,这样做的好处是 
【实验结论】
如图所示,他们进行了三次实验,对实验数据进行分析,得出杠杆的平衡条件是 ,
【拓展应用】如图所示,是用手托起重物的示意图,图中前臂可以看作是一个 杠杆(选填“省力”、“费力”或“等臂”),此杠杆的支点是图中的 点,假如托起6N的重物,请你根据图21所示,估算出手臂要用的动力大约是 N
如图甲是一台落地电风扇,电风扇的参数见下表;乙图是电风扇的尺寸示意图,由于电风扇的质量分布不均匀,它的重力作用点在P点;电风扇内部的电路图可简化为丙图,图中的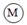 代表电动机,R1、R2是限流电阻。
代表电动机,R1、R2是限流电阻。
(1)小明想在电路中加一个“倾倒开关”,使电风扇被碰倾倒时能自动断开电路。此开关应该安装在丙图中的 (选填“A”、“B”或“C”)处。
(2)将电风扇调到最高档(最大风速),H调到最大值,此时H=120cm,它的放置状态如图乙所示,在水平方向扇叶受到空气对它向左的作用力F=16N,重力作用点P离电风扇底座中轴线横向距离a=15cm,P点离地面的距离b=40cm,底座半径r为17 cm。当电风扇的风速达到最大时,它会翻倒吗?请用杠杆平衡原理计算说明。(g=10N/Kg)
(3)电风扇在额定电压下工作,当旋转开关调到2位置时,风速档位是 (选填“低档”、“中档”或“高档”);此时,电动机两端的电压为100V,求R1的阻值及电动机的输出功率。
小梅在物理老师的指导下,利用一个重物、细线、若干钩码及杠杆来探究“杠杆平衡的条件”。
(1)实验前,为便于力臂的测量,她应通过调节杠杆两端的 使杠杆在 位置平衡。
(2)实验时,小梅决定先保持阻力 和阻力臂 不变,探究“杠杆平衡时,动力臂和动力之间的关系”。
于是,她用细线将重物固定到杠杆左侧某一位置处;然后在杠杆右侧用细线悬挂一个钩码,移动其悬挂的位置,使杠杆重新在水平位置平衡,如图所示,将动力 和动力臂 记录下来。
接下来,她要改变 并移动其悬挂的位置,多次重复前面的实验,并把相应的数据记录下来。
(3)小梅通过实验得到的实验数据如表1所示。
表一 保持阻力 和阻力臂 不变,探究杠杆平衡时动力臂和动力之间的关系
实验序号 |
动力 |
动力臂 |
1 |
0.5 |
0.20 |
2 |
1.0 |
0.10 |
3 |
1.5 |
0.07 |
4 |
2.0 |
0.05 |
5 |
2.5 |
0.04 |
分析表1中的数据,小梅得出的结论是:保持阻力和阻力臂不变,杠杆平衡时,动力臂 跟动力 成 关系。
(4)在前面实验的基础上,小梅进一步猜想:在更普遍的情况下,杠杆平衡时可能满足“动力 动力臂 阻力臂 阻力臂 ”
为了验证小梅的这个猜想,小丽通过实验得到的实验数据如表2所示
表2 探究杠杆平衡时,动力 、动力臂 和阻力 、阻力臂 之间的关系
实验次数 |
动力 |
动力臂 |
阻力 |
阻力臂 |
1 |
1.0 |
0.10 |
1.0 |
0.10 |
2 |
1.5 |
0.08 |
1.5 |
0.08 |
3 |
2.0 |
0.07 |
2.0 |
0.07 |
小梅认为,表2中小丽的实验数据缺乏普遍性,用来验证她的猜想不够充分,于是对小丽的实验和收集数据提出了具体的建议。
小梅的建议是:小丽还要在 的情况下进行实验和收集数据。
如图,杠杆处于平衡状态,如果在杠杆两侧挂钩码处各增加一个质量相同的钩码,杠杆会
| A.左端下降 |
| B.右端下降 |
| C.仍然平衡 |
| D.无法判断 |
如图所示,某同学在做俯卧撑运动,可将他视为一个杠杆,支点在O点,他的重心在A点,重力为600N.
求:(1)他将身体撑起时,地面对双手的支持力至少多大?
(2)若他在1min内做了30个俯卧撑,每次肩部上升的距离均为0.4m,则他做一个俯卧撑要做多少功?
(3)他做俯卧撑的功率为多少瓦?
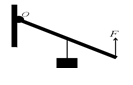
(1)如图所示是右侧带书柜的办公桌,我们可以把它抽象成一个“杠杆”.现在要用一个最小的力将这张办公桌的一端稍抬离地面.请画出这个力F和这个力臂l,并用“O”标明这个“杠杆”的支点.
(2)在右图中画出斜面上“不倒翁”受重力的示意图,并画出重力相对于支点O的力臂l 1. (黑点表示“不倒翁”的重心)
如图甲长2m的粗细和密度都均匀的光滑金属杆可绕O点转动,杆上有一光滑滑环,用竖直向上的测力计拉着滑环缓慢向右移动,使杆保持水平状态,测力计示数F与滑环离开O点的距离S的关系如图所示,则杆重 N;当滑环滑到图中A点时,金属杆是一个 杠杆(选填“省力”、“费力”或“等臂”).
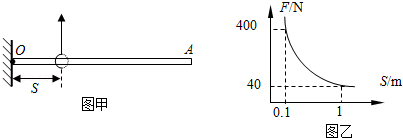
(1)如图1甲所示的钢丝钳,其中A是剪钢丝处,B为手的用力点,O为转动轴(支点),图乙为单侧钳柄及相连部分示意图.请在图乙中画出钢丝钳剪钢丝时的动力臂L1,并在A点作出阻力F2.
(2)如图2所示,在杠杆AB上挂了一个重为G的物体.为使杠杆在图中的位置静止,请在杠杆上画出最小的动力F;
(3)用如图3所示的滑轮组提升一重物有两种绕绳方法,请画出最省力的一种.
(4)请在图4中的两个虚线框内,选填“电源”和“开关”的符号,并满足当开关都闭合时两灯组成并联电路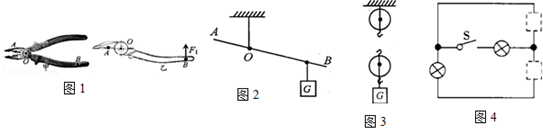
如图所示,用竖直向上的力F匀速拉动较长的杠杆,使重为10N的物体缓慢升高0.1m,拉力大小为8N,拉力移动的距离为0.25m。人做的有用功为_ J,该杠杆的机械效率为 ,此杠杆属于 (选填“省力”、“费力”或“等臂”)杠杆。
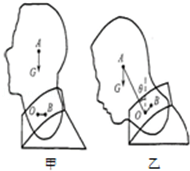
“低头族”长时间低头看手机,会引起颈部肌肉损伤.当头颅为竖直状态时,颈部肌肉的拉力为零,当头颅低下时,颈部肌肉会产生一定的拉力.为了研究颈部肌肉的拉力与低头角度大小的关系,我们可以建立一个头颅模型来模拟实验,如图甲所示.把人的颈椎简化成一个支点O,用1kg的头颅模型在重力作用下绕着这个支点O转动,A点为头颅模型的重心,B点为肌肉拉力作用点.将细线的一端固定在B点,用弹簧测力计拉着细线模拟测量肌肉的拉力,头颅模型在转动过程中,细线拉力的方向始终垂直于OB,如图乙所示.让头颅模型从竖直状态开始转动,通过实验记录出低头角度θ及细线拉力F的数据.如表:
| 低头角度θ/° |
0 |
15 |
30 |
45 |
60 |
| 细线拉力F/N |
0 |
7.3 |
14.0 |
20.2 |
25.0 |
(1)头颅模型质量为1kg,当低头角度为60°时,颈部肌肉实际承受的拉力是 N;如果真实头颅质量为8kg,当低头角度为60°时,颈部肌肉实际承受的拉力是 N.
(2)请解释:为什么低头角度越大,颈部肌肉的拉力会越大?答 .
(3)请你就预防和延缓颈椎损伤提出一个合理化的建议: .
如图所示,可绕O点转动的轻质杠杆,在D点挂一个重为G的物体M.用一把弹簧测力计依次在A、B、C三点沿与圆O相切的方向用力拉,都使杠杆在水平位置平衡,读出三次的示数分别为F1、F2、F3,它们的大小关系是( )

A.F1<F2<F3<G B.F1>F2>F3>G
C. F1>F2=F3=G D.F1=F2=F3=G
如图所示,O为杠杆的支点,在杠杆的右端B点挂一重物。MN是以A为圆心的弧形导轨,绳的一端系在杠杆的A点,另一端E可以在弧形导轨上自由滑动。当绳的E端从导轨的一端N点向另一端M点滑动的过程中,杠杆始终水平,绳AE对杠杆拉力的变化情况:( )

| A.先变小,后变大 | B.先变大,后变小 |
| C.一直变小 | D.一直变大 |
如图所示,有一轻质木板(质量忽略不计),左端可绕O点转动,长为L,右端放一重为G的物块,并用一竖直向上的力F拉着.当物块向左匀速滑动时,木板始终在水平位置保持静止,则下列表示拉力F与物块运动时间t的关系图中,正确的是( )

A.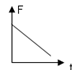 B.
B. C.
C.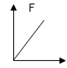 D
D